Несобственные интегралы первого рода.
Могут встретиться три типа бесконечных областей:
1) полупрямая 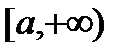
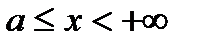
2) полупрямая 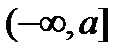
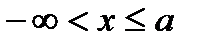
3) вся бесконечная прямая 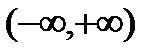
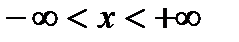
Рассмотрим функцию 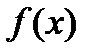 , определенную на полупрямой
, определенную на полупрямой 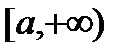 . Пусть A- некоторая точка полупрямой, большая чем а(A>a) и пусть функция
. Пусть A- некоторая точка полупрямой, большая чем а(A>a) и пусть функция 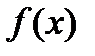 интегрируема на отрезке
интегрируема на отрезке 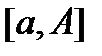 , принадлежащим рассматриваемой полупрямой. Тогда на полупрямой можно рассмотреть функцию
, принадлежащим рассматриваемой полупрямой. Тогда на полупрямой можно рассмотреть функцию
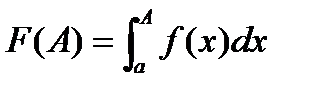 (1).
(1).
Определение: Предел функции 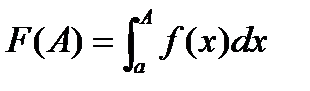 при
при 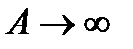 , если он существует, называется несобственным интегралом первого рода от функции
, если он существует, называется несобственным интегралом первого рода от функции 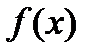 по полупрямой
по полупрямой 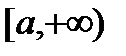 и обозначается
и обозначается
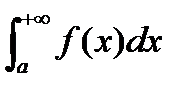 (2).
(2).
При этом говорят, что несобственный интеграл (2) сходится. Если предел бесконечен или не существует, то говорят, что несобственный интеграл расходится. Таким образом:
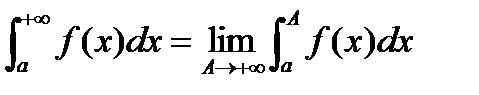 (3).
(3).
Пример1: Для тела, полученного вращением гиперболы x*y=1 вокруг оси ох вычислить объем и боковую поверхность части, определяемой неравенством: 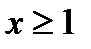 .
.
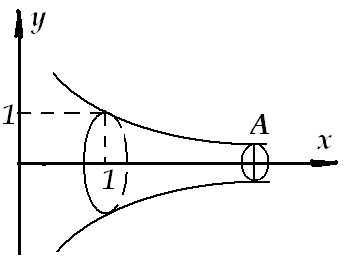
Возьмем некоторое значение A и вычислим объем тела на отрезке 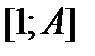
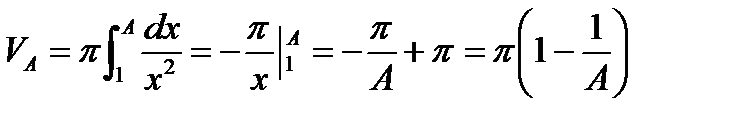
Естественно под 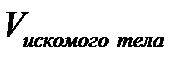 подразумеваем предел:
подразумеваем предел: 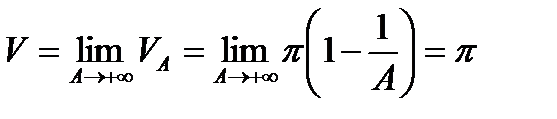 , т.е.
, т.е. 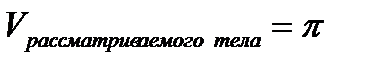 .
.
Решим вопрос о площади боковой поверхности бесконечного тела. 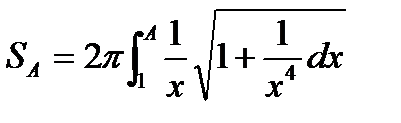 .
.
Очевидно, что функция 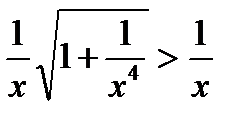 =>
=> 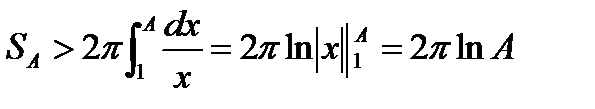 .
.
Таким образом, получаем, что 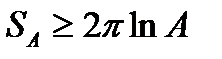 . Переходя к пределу, получим, что S рассматриваемого тела будет бесконечно большой: Таким образом, интеграл, задающий S рассматриваемого тела, расходится.
. Переходя к пределу, получим, что S рассматриваемого тела будет бесконечно большой: Таким образом, интеграл, задающий S рассматриваемого тела, расходится.
Пример2: Если в электрической цепи с самоиндукцией в момент времени t=0 ток силы 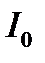 разомкнуть, то в цепи возникнет экстра ток размыкания
разомкнуть, то в цепи возникнет экстра ток размыкания 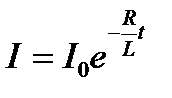 . Вычислить полное количество теплоты выделяемое этим током. Количество тепла, выделяемое на отрезке
. Вычислить полное количество теплоты выделяемое этим током. Количество тепла, выделяемое на отрезке 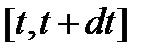 определяется выражением:
определяется выражением:
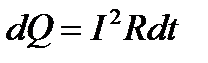 , тогда всё джоулевое тепло будет определяться:
, тогда всё джоулевое тепло будет определяться: 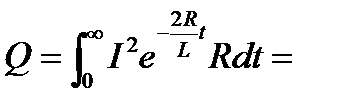
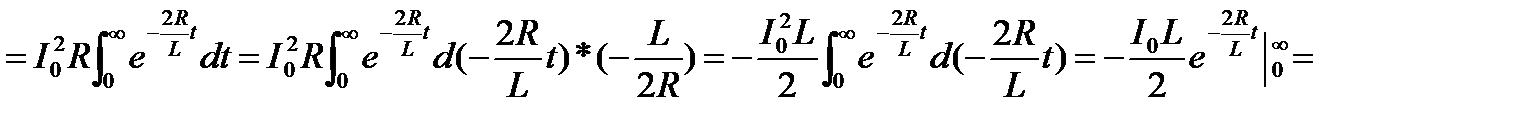
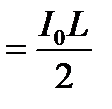 .
.
Аналогично с определением несобственного интеграла от 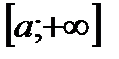 , вводится понятия несобственного интеграла от
, вводится понятия несобственного интеграла от 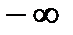 до
до 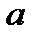 , этот интеграл принято обозначать
, этот интеграл принято обозначать 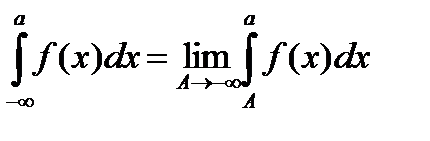 . Если рассматривается вся числовая прямая от
. Если рассматривается вся числовая прямая от 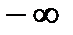 до
до 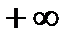 , то несобственный интеграл записывается в виде:
, то несобственный интеграл записывается в виде:
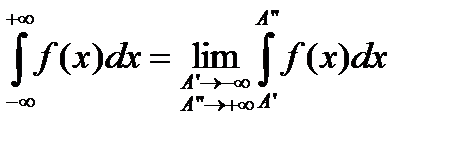 причём
причём 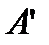 и
и 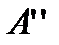 стремиться к бесконечностям не зависимо друг от друга. Из этих определений следует, что если для некоторого числа
стремиться к бесконечностям не зависимо друг от друга. Из этих определений следует, что если для некоторого числа 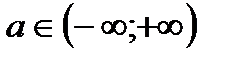 сходятся несобственные интегралы
сходятся несобственные интегралы 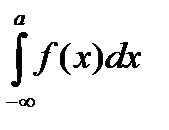 и
и 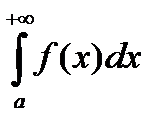 , то будет сходится
, то будет сходится 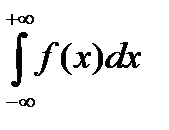 и имеет место равенство
и имеет место равенство 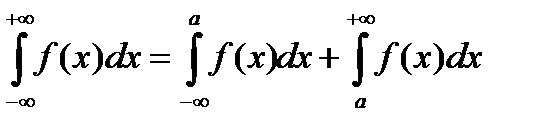 .
.
Отметим также, если сходится 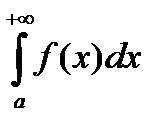 и
и 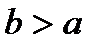 - некоторые число, то сходится интеграл
- некоторые число, то сходится интеграл 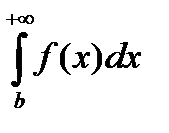 , причём имеет место равенство
, причём имеет место равенство 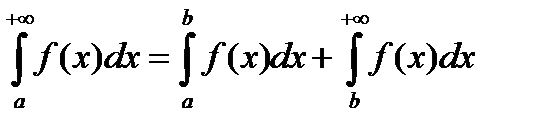
Дата добавления: 2017-06-13; просмотров: 1339;











