Площадь криволинейного сектора

В полярной системе координат положение точки на плоскости определяется парой чисел: 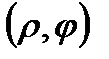. Число 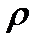определяет расстояние от точки М до полюса. 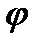- угол образованный отрезком ОМ и полярной осью.

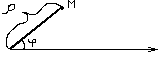
Если полюс совпадает с началом декартовой системы координат, а ось х совпадает с полярной осью, то между декартовой и полярной системами координат, существует связь.

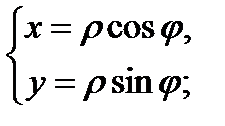
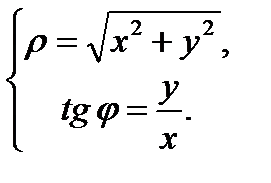
При нахождении 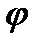нужно учитывать, в какой четверти находится точка, и брать соответствующее значение.

В полярной системе координат уравнение кривой может быть записано в виде

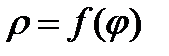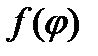где - непрерывная функция, .

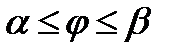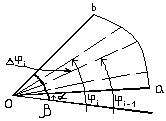
Находясь в полярной системе координат, получим выражение для площади сектора ОАВ ограниченного кривой 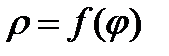и радиус векторами 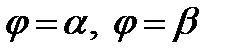. Разобьём данную область радиус – векторами 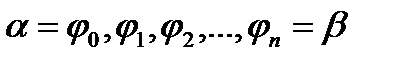на n – частей. Обозначим через 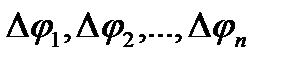- углы между радиус векторами.

Обозначим через 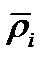-некоторый радиус-вектор, соответствующий углу , .

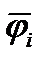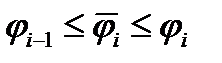Рассмотрим круговой сектор с радиусом 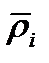и центральным углом 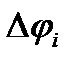. Площадь кругового сектора равна: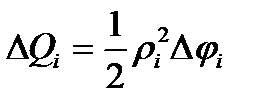

Сумма 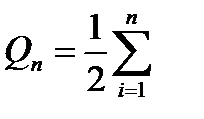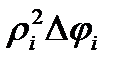= 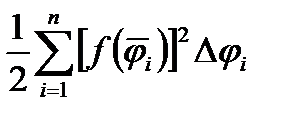даёт площадь ступенчатого сектора. Так как эта сумма является интегральной суммой для функции 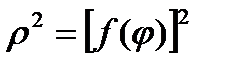на отрезке 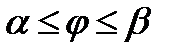, то её предел есть неопределённый интеграл 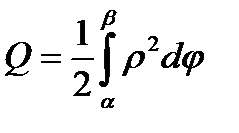. Выписанный интеграл считают площадью криволинейного сектора ОАВ.

Длина дуги кривой