Несобственный интеграл второго рода.

Пусть 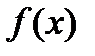задана на 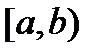и не ограниченна на нём, и пусть, кроме того 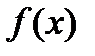- ограничена и интегрируема на любом отрезке 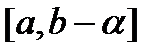, , 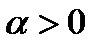целиком содержащемся в 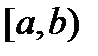. Точка 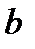в полусегменте 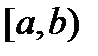называется особой точкой функции .

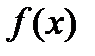На полусегменте 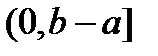рассмотрим функцию аргумента 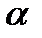, определяемую соотношением 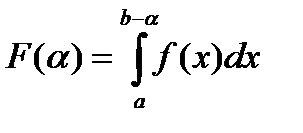(1).

Определение: Правый предел функции (1) 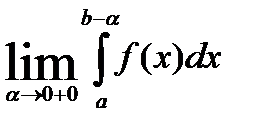при условии, что он существует, называется несобственным интегралом второго рода.

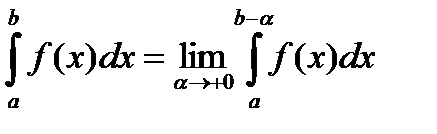(2)

Если предел (2) существует, то говорят, что интеграл сходиться, если конечный предел не существует, то интеграл расходится.

Пример: 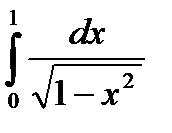- видим, что подынтегральная функция не ограничена при .

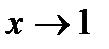1-является особой точкой подынтегральной функции. Функция интегрируема на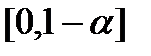

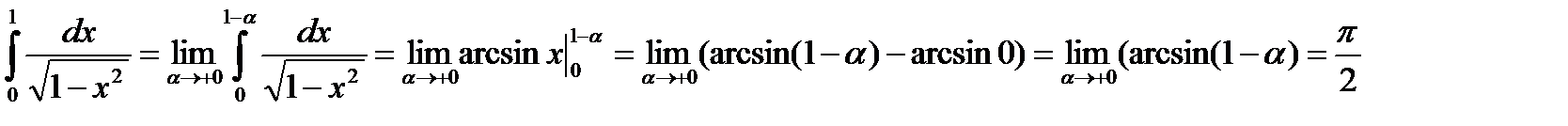
Если функция определена на 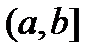и точка 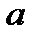является особой точкой функции, то несобственный интеграл определяется выражением:

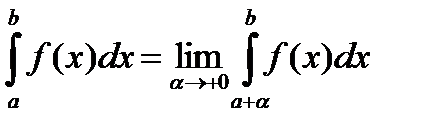
Пример: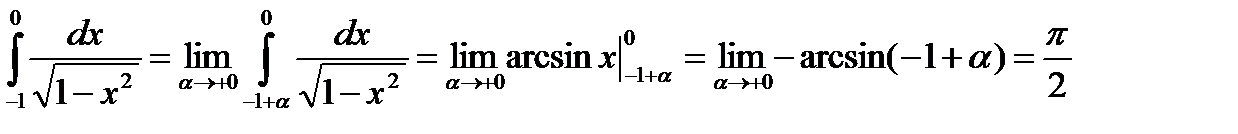

В общем случае в промежутке [a,b] может быть конечное число особых точек 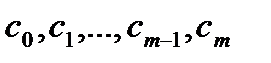, вблизи которых функция f(x) неограниченна, но в каждой части отрезка [a,b] не содержащей особых точек, функция ограничена и интегрируема.

Пример: Пусть дана такая функция на 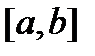и особыми точками являются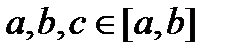

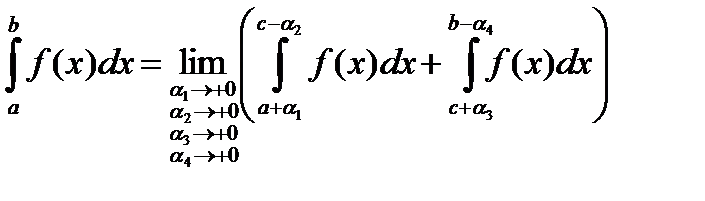(3)

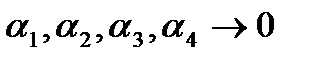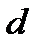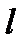Где независимо друг от друга. Взяв по точке и , где 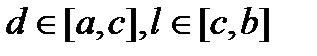выражение (3), можно переписать в виде:

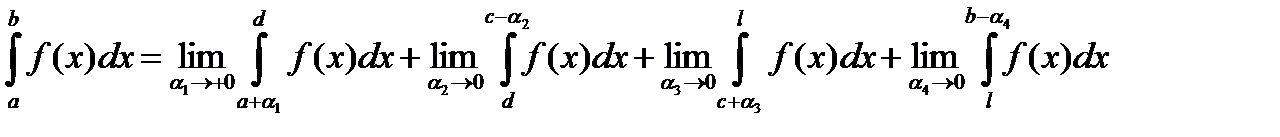(4)

Таким образом, замечаем, что несобственный интеграл (3) существует, если существует четыре несобственных интеграла, выписанных в правой части (4)

Пример: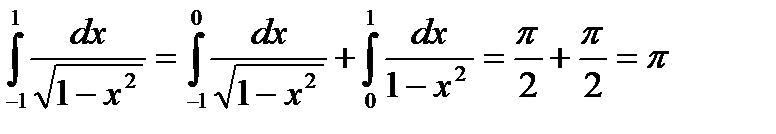

Признаки сходимости несобственных интегралов второго рода аналогичны признакам сходимости несобственных интегралов первого рода. Во многих случаях с помощью замены переменной, несобственный интеграл второго рода можно преобразовать к несобственному интегралу первого рода.

Рассмотрим функцию 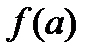на 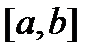пусть b – особая точка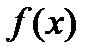

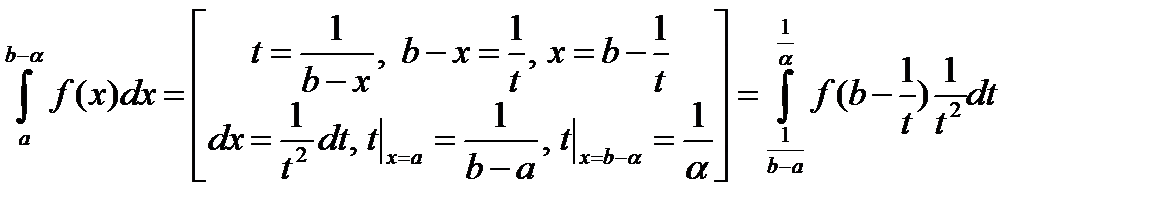
Переходя к 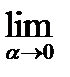слева 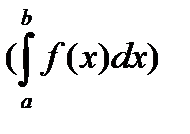получим несобственный интеграл второго рода, а в правой части интеграл первого рода .

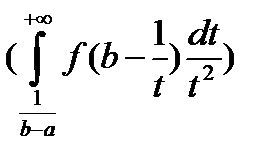Если сходится один из этих интегралов, то сходится и другой, то есть, оба интеграла сходятся и расходятся одновременно.