Длина дуги, заданная параметрически.
Пусть кривая задана параметрически 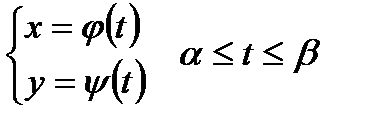
причем 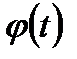 и
и 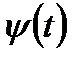 , обладают непрерывными производными на отрезке
, обладают непрерывными производными на отрезке 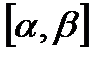 , причем
, причем 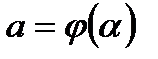 ,
, 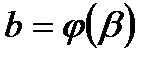 . Ранее было показано, что длина дуги, заданная явным уравнением, определяется интегралом:
. Ранее было показано, что длина дуги, заданная явным уравнением, определяется интегралом: 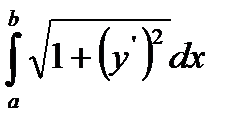 . Производная
. Производная 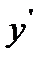 -функции заданной параметрическими вычисляется в виде:
-функции заданной параметрическими вычисляется в виде: 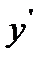 =
= 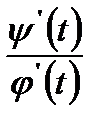 . Перейдем в определенном интеграле от переменной х к переменной t, в результате получим:
. Перейдем в определенном интеграле от переменной х к переменной t, в результате получим: 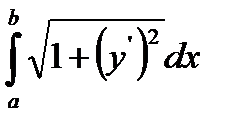 =
= 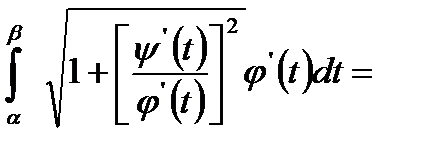
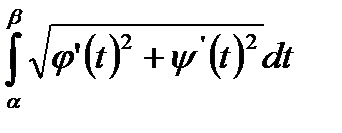 , таким образом, длина дуги заданная параметрически, определяется интегралом:
, таким образом, длина дуги заданная параметрически, определяется интегралом: 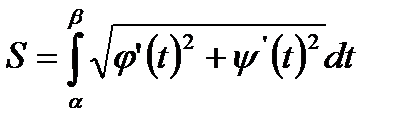 .
.
Пример:Вычислить длину астроиды. Уравнение астроиды имеет вид: 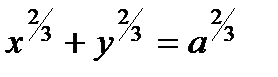 .
.
Астроида получается при движении точки окружности радиуса r, при качении её по внутренней стороне окружности радиуса R=4r.
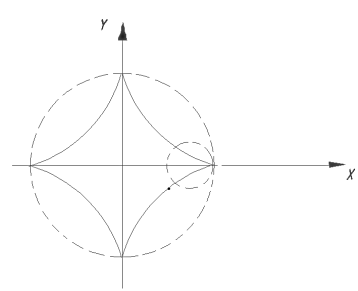 Используя основное тригонометрическое тождество
Используя основное тригонометрическое тождество 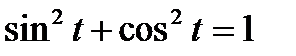 , введем параметризацию астроиды:
, введем параметризацию астроиды:
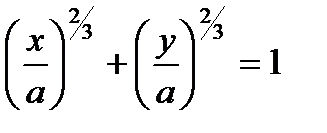 ,
, 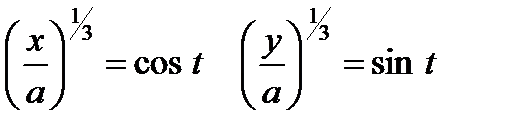 . Таким образом получаем,
. Таким образом получаем, 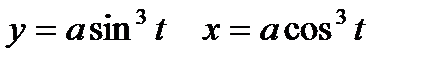 . Уравнение астроиды симметрично относительно начала координат, и для вычисления длины астроиды, вычислим длину дуги в первой четверти и умножим на 4.
. Уравнение астроиды симметрично относительно начала координат, и для вычисления длины астроиды, вычислим длину дуги в первой четверти и умножим на 4.
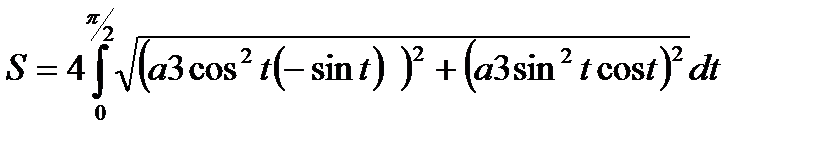
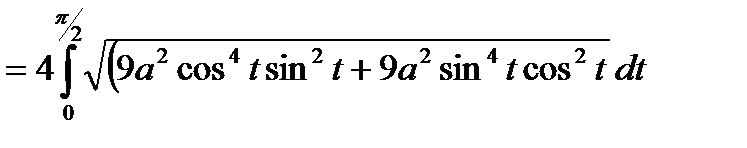 =
= 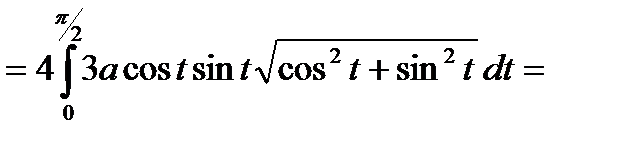
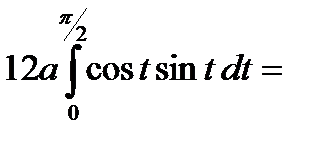
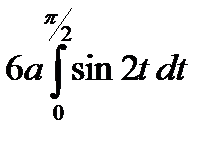
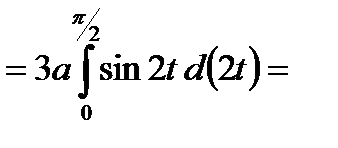
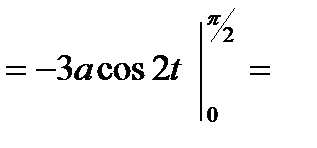
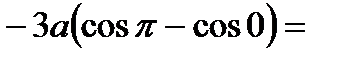
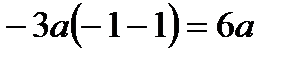 .
.
В случае кривой заданной параметрически в трехмерном пространстве:
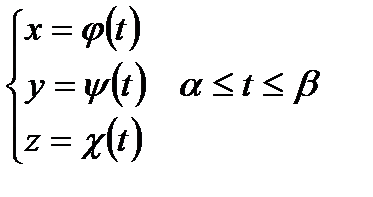 .
.
Длина кривой определяется формулой:
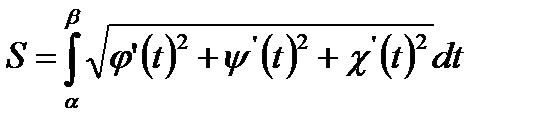 .
.
Дата добавления: 2017-06-13; просмотров: 3067;











