Длина дуги кривой в декартовой прямоугольной системе координат.
Пусть в прямоугольных координатах на плоскости дана кривая  заданная на отрезке
заданная на отрезке 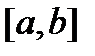 . Функция
. Функция 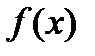 - обладает непрерывной производной на отрезке
- обладает непрерывной производной на отрезке 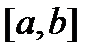 . Найдём длину дуги АВ этой кривой, заключённой между вертикальными прямыми
. Найдём длину дуги АВ этой кривой, заключённой между вертикальными прямыми 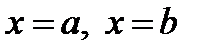 . Возьмём на дуге АВ точки
. Возьмём на дуге АВ точки 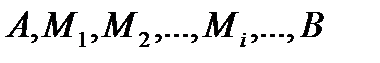 с абсциссами
с абсциссами 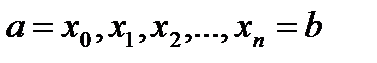 .
.
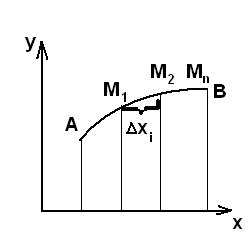 Соединим выбранные точки хордами, получим ломаную линию, вписанную в дугу
Соединим выбранные точки хордами, получим ломаную линию, вписанную в дугу 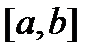 .
.
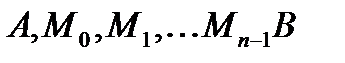 . длина ломаной
. длина ломаной 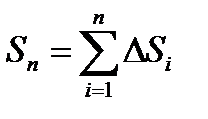 . Длиной S дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю.
. Длиной S дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю.
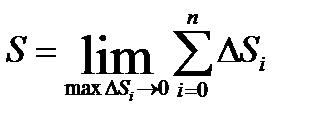 .
.
Покажем, что предел существует.
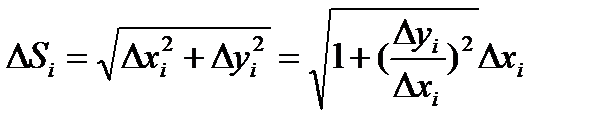
Рассматриваемая функция 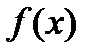 удовлетворяет всем условиям теоремы Лагранжа. Согласно этой теоремы
удовлетворяет всем условиям теоремы Лагранжа. Согласно этой теоремы 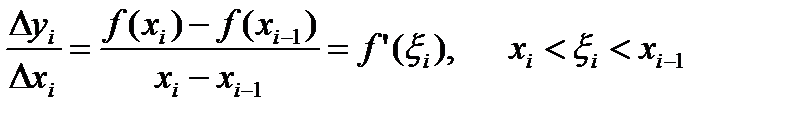 .
.
Следовательно, 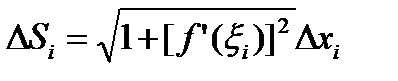 .
.
Таким образом, длина ломаной равна 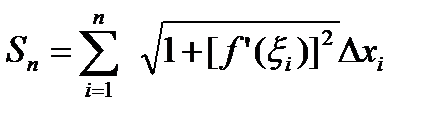 .
.
Выписанную сумму можно рассматривать как интегральную сумму на отрезке 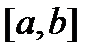 . Функция стоящая под знаком суммы непрерывна, согласно сделанным предположениям, и следовательно существует предел интегральной суммы, который равен определённому интегралу
. Функция стоящая под знаком суммы непрерывна, согласно сделанным предположениям, и следовательно существует предел интегральной суммы, который равен определённому интегралу 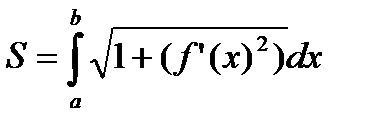
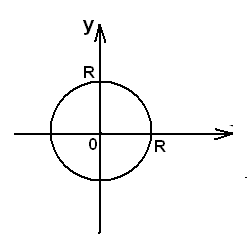 Пример:Вычислить длину окружности
Пример:Вычислить длину окружности
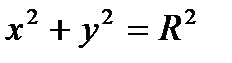
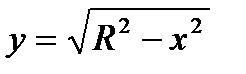
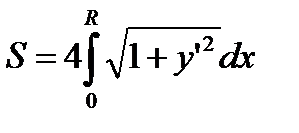
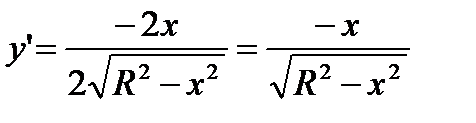 .
.
Следовательно, 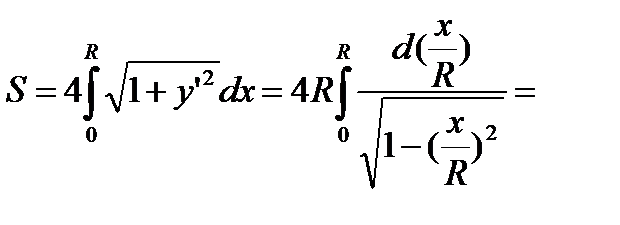

Дата добавления: 2017-06-13; просмотров: 1853;











