АКСИОМЫ СТЕРЕОМЕТРИИ
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «стереос» – объемный, пространственный и «метрео» – измерять.
Представление о геометрических телах, изучаемых в стереометрии, дают окружающие нас предметы. В отличие от реальных предметов геометрические тела являются воображаемыми объектами. Изучая свойства геометрических тел, мы получаем представление о геометрических свойствах реальных предметов и можем использовать эти свойства в практической деятельности. Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
Схема построения геометрии
Перечисляются основные неопределяемые понятия.
Формулируются свойства основных понятий - аксиомы.
Определяются другие геометрические понятия.
Формулируются и доказываются свойства геометрических понятий - теоремы.
АКСИОМЫ СТЕРЕОМЕТРИИ. СЛЕДСТВИЯ ИЗ АКСИОМ
Основные понятия стереометрии: точка, прямая, плоскость, расстояние.
Определение: Аксиомой называется предложение, не требующее доказательства.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, известных нам по курсу планиметрии, и аксиом о взаимном расположении точек, прямых и плоскостей в пространстве.
АКСИОМЫ СТЕРЕОМЕТРИИ
I. Аксиомы принадлежности
I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.
Обозначение:
А, В, С, D – точки;
а, b, с – прямые;
a , b , g – плоскости;
А Î а – точка А принадлежит прямой а, прямая а проходит через точку А;
Е Ï а – точка Е не принадлежит прямой а;
С Î a – точка С принадлежит плоскости a , плоскость a проходит через точку С;
Е Ï a – точка Е не принадлежит плоскости a .
Вывод: Существуют точки, принадлежащие прямой и не принадлежащие прямой, существуют точки, принадлежащие плоскости и не принадлежащие плоскости.
I2. Через две различные точки проходит одна и только одна прямая.
 |
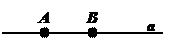Обозначение: а = АВ
Вывод: Прямые, имеющие две различные общие точки, совпадают.
I3. Прямая, проходящая через две любые точки плоскости, лежит в этой плоскости.
 |
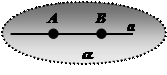Обозначение:
а Ì a – плоскость a проходит через прямую а;
b Ë a – плоскость a не проходит через прямую b.
I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
Обозначение: a = АВС
Вывод: Плоскости, имеющие три различные общие точки, совпадают.
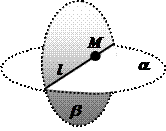
I5. Если две различные плоскости имеют общую точку, то их пересечением является прямая.
Обозначение: М Î a , М Î b , a ¹ b , a ìüb = l.
II. Аксиомы расстояния
II1. Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние АВ равно нулю тогда и только тогда, когда точки А и В совпадают.
 |
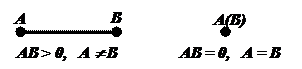Обозначение: АВ ³ 0.
II2. Расстояние от А до В равно расстоянию от В до А.
Обозначение: АВ = ВА.
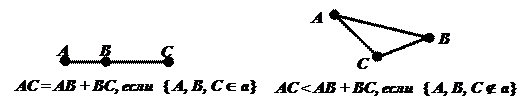II3. Для любых трех точек А, В, С расстояние от А до С не больше суммы расстояний от А до В и от В до С.
Обозначение: АС £ АВ + ВС .
III. Аксиомы порядка
III1. Любая точка О прямой р разбивает множество всех отличных от точки О точек прямой р на два непустых множества так, что для любых двух точек А и В, принадлежащим разным множествам, точка О лежит между точками А и В; если точки А и В принадлежат одному и тому же множеству, то одна из них лежит между другой и точкой О.
 |
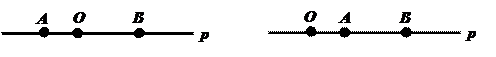III2. Для любого расстояния а на заданном луче с началом О существует одна и только одна точка А, расстояние от которой до точки О равно а.
 |
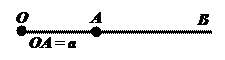III3. Если точка С лежит между точками А и В, то точки А, В, С принадлежат одной прямой.
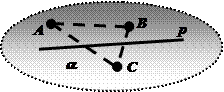III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
IV. Аксиома подвижности плоскости
Если точки А, В, А1, В1 лежат в плоскости a, причем АВ > 0 и АВ = А1В1, то существует два и только два перемещения этой плоскости, каждое из которых отображает точку А на точку А1 а точку В на точку В1.
V. Аксиома параллельных
Через точку А проходит не более одной прямой, параллельной данной прямой р.
Дата добавления: 2017-05-02; просмотров: 6108;
Поиск по сайту
Узнать еще
- Аксиомы межличностной коммуникации
- Аксиомы теории вероятностей
- Аксиомы теории вероятностей. Дискретные пространства элементарных исходов. Классическое определение вероятности
- Аксиомы, законы, тождества и теоремы алгебры логики
- Введение в механику. Основные понятия и аксиомы статики
- Основные аксиомы статики
- Основные правила комбинаторики. Выборки, сочетания. Аксиомы теории вероятностей
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
