Существование плоскости a , проходящей через две параллельные прямые а и b, следует из определения параллельных прямых.
2. Предположим, что существует другая плоскость, содержащая прямые а и b. Выберем на прямой а точку А, на прямой b точки В и М (аксиома I1): АÎа, ВÎb, МÎb. Получили, что через точки А, В, М проходят две плоскости, что противоречит аксиоме I4. Следовательно, предположение не верно, плоскость а – единственная.
Упражнения:
1. Прочитать запись и сделать схематический рисунок:
a) 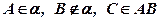 ;
;
b) 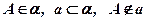 ;
;
c) 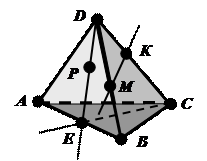
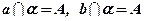 ;
;
d) 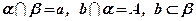 .
.
2. По рисунку назвать:
a) плоскости, в которых лежат прямые РЕ, МК, DВ, АВ, ЕС;
b) точки пересечения прямой DК с плоскостью АВС, прямой СЕ с плоскостью АDВ;
c) точки, лежащие в плоскостях АDВ и DВС;
d) 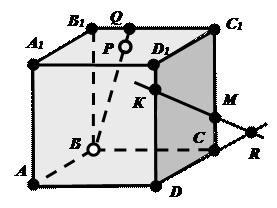 прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС.
прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС.
3. По рисунку назвать:
a) точки, лежащие в плоскостях DСС1 и ВQС;
b) плоскости, в которых лежит прямая АА1;
c) точки пересечения прямой МК с плоскостью АВD, прямых DК и ВР с плоскостью А1В1С1;
d) прямые, по которым пересекаются плоскости АА1В1 и АСD, РВ1С1 и АВС;
e) точки пересечения прямых МК и DС, В1С1 и ВР, С1М и DС.
2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ В ПРОСТРАНСТВЕ
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ
Дата добавления: 2017-05-02; просмотров: 2719;











