Дифференциальные уравнения плоского движения твёрдого тела.

***

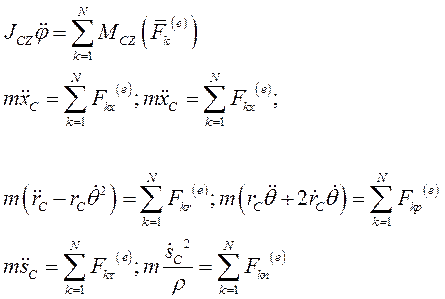
Дифф. уравнения плоского движения твёрдого тела получим на основании теорем о движении центра масс и об изменении главного момента количеств движения в относительном движении по отношению к центру масс.

В неподвижной системе Oxyz координат согласно 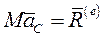для центра масс будем иметь

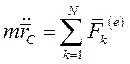(I)

Введем подвижную СК CXYZ, имеющую начало в ЦМ тела и перемещающуюся относительно системы Oxyz поступательно, причем плоскости Oxy и CXY будем считать совпадающими с плоскостью, в которой движется ЦМ. Теорема об изменении момента количеств движения в относительном движении по отношению к ЦМ в проекции на CZ подвижной СК:

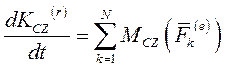
в уравнении главный момент количеств движения тела в его относительном вращении вокруг оси CZ подвижной СК

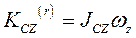
Следовательно, дифф. уравнение, описывающее вращение твёрдого тела относительно оси CZ, имеет вид

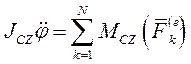(II)

Эти два уравнения (I),(II) полностью описывают плоское движение твёрдого тела.

В проекциях на оси полярной СК:

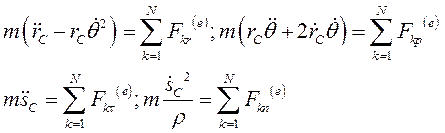
Где 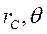- полярные координаты центра масс тела в неподвижной системе отсчёта. 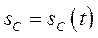- закон движения центра масс по траектории.

Начальные условия в общем случае:

При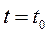

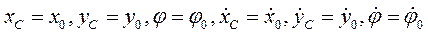
или

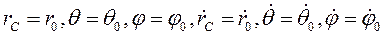
или

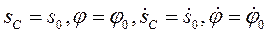
В зависимости от числа степеней свободы тела для описания его плоского движения можно использовать от одной до трёх обобщенных координат, используемые в приведённых выше уравнениях и начальных условиях.