Теорема об изменении кинетического момента для точки и системы материальных точек. Законы сохранения кинетического момента.
Первая производная по времени от момента количества движения точки относительно центра О равна моменту равнодействующей силы относительно того же центра О.
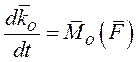
|
Уравнение движения мат. точки::
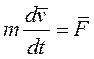
умножим его векторно слева на радиус-вектор
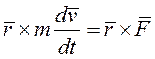
Преобразуем левую часть полученного уравнения
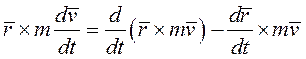
Но 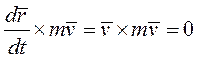 как векторное произведение коллинеарных векторов.
как векторное произведение коллинеарных векторов.
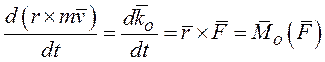
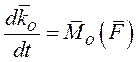
Первая производная по времени от главного момента количеств движения механической системы относительно неподвижного центра О равна главному моменту внешних сил, приложенных к точкам системы, относительно того же центра.
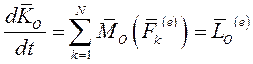 (9) (9)
|
Рассмотрим мех. систему 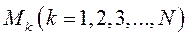 из N материальных точек, к каждой из которых приложены равнодействующие внешних и внутренних сил. Для каждой точки
из N материальных точек, к каждой из которых приложены равнодействующие внешних и внутренних сил. Для каждой точки 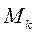 запишем теорему об изменении момента количества движения относительно неподвижного центра О.
запишем теорему об изменении момента количества движения относительно неподвижного центра О.
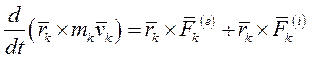
Просуммировав по всем точкам
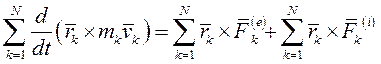
и преобразовав левую часть уравнения получим:
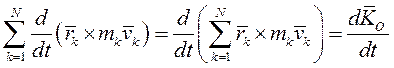
Здесь 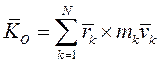 - главный момент количеств движения механической системы относительно центра О.
- главный момент количеств движения механической системы относительно центра О.
Главный момент внутренних сил
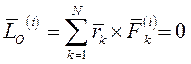
а главный момент внешних сил
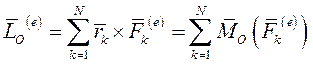
Окончательно имеем: 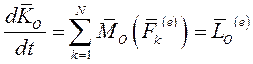 (9)
(9)
Законы сохранения:
1. Закон сохранения главного момента количеств движения механической системы относительно центра О в векторной форме:
Если главный момент внешних сил относительно неподвижного центра О равен нулю, то главный момент количеств движения механической системы относительно этого центра постоянен по модулю и направлению.
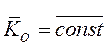
|
Пусть главный момент внешних сил системы относительно центра О равен нулю, т.е. 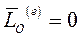 . Тогда, согласно (9)
. Тогда, согласно (9)
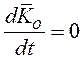
Интегрируя, получаем
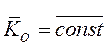
2. Если главный момент внешних сил, действующих на механическую систему, относительно какой-либо оси равен нулю, то главный момент количеств движения механической системы относительно этой оси постоянен.
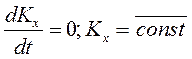
|
Пусть сумма внешних моментов внешних сил, действующих на механическую систему, относительно оси Ох равна нулю, т.е. 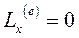 . Тогда
. Тогда
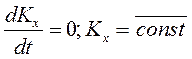
Если рассматривается тело или система тел, вращающихся вокруг неподвижной оси Оz с угловой скоростью 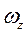 и
и 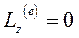 , то
, то 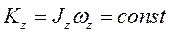 .
.
Дата добавления: 2021-07-22; просмотров: 489;











