Кинетический момент системы материальных точек при сложном движении.
Главный момент количеств движения механической системы относительно неподвижного центра О для абсолютного движения системы равен векторной сумме момента вектора количество абсолютного движения системы (приложенного в центре масс) относительно того же центра, и главного момента количеств движения системы относительно центра масс для относительного движения системы по отношению к центру масс
.
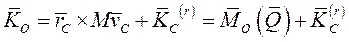 (11)
В проекции на ось OZ: (11)
В проекции на ось OZ:
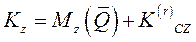
|
Введем подвижную систему координат CXYZ, которая двигается поступательно по отношению к инерциальной системе отсчета Оxyz и начало которой связано с центром масс С системы. Подвижную СК CXYZ называют кенинговой системой координат. продифференцируем по времени выражение 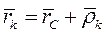
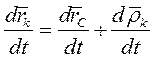
Тогда
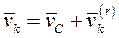
Согласно формуле Бура
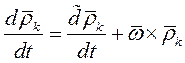
Но при поступательном движении системы CXYZ
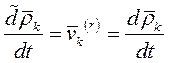
Главный момент кол-ва движения мех. системы относительно неподвижного центра О для абсолютного движения системы относительно неподвижной (инерциальной) системы координат Oxyz равен
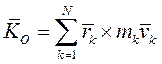
Подставляя сюда выражения для 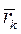 и
и 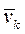
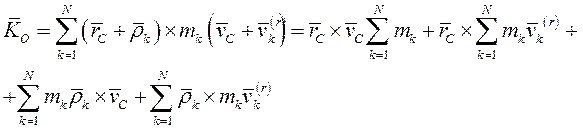
Здесь 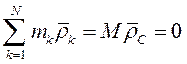 так как радиус-вектор центра масс относительно центра масс
так как радиус-вектор центра масс относительно центра масс 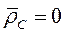 , а следовательно
, а следовательно
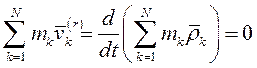
Т.е. количество движения системы в её движении относительно центра масс равно нулю.
Таким образом:
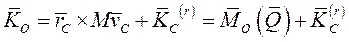 (11)
(11)
Где 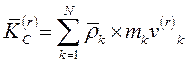 - главный момент количеств движения мех. системы относительно центра масс для относительного движения системы по отношению к центру масс (по отношению к СК CXYZ, движущейся поступательно вместе с центром масс)
- главный момент количеств движения мех. системы относительно центра масс для относительного движения системы по отношению к центру масс (по отношению к СК CXYZ, движущейся поступательно вместе с центром масс)
В проекции на ось Oz (CZ) формула (11) принимает вид
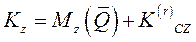
Дата добавления: 2021-07-22; просмотров: 571;











