Работа сил, приложенных к твёрдому телу при его различных движениях.

Работа силы при поступательном движении твёрдого тела.

При поступательном движении твёрдого тела векторы скоростей, а также элементарные перемещения всех точек тела одинаковы. Тогда элементарная работы силы

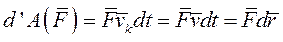
Полная работа силы на каком-либо перемещении

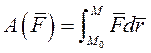
Работа силы при вращении твёрдого тела вокруг неподвижной оси.

Элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела

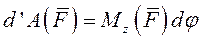
Полная работа:

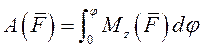
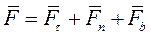
Работы составляющих силы по нормали и бинормали равны нулю, так как они направлены всегда перпендикулярно к вектору скорости точки М приложения силы. Следовательно, элементарная работа силы 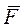совершается только её составляющей 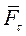по касательной к траектории, т.е.

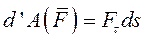
Поскольку 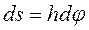, то

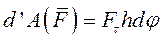
Где h – кратчайшее расстояние от точки приложения силы до оси вращения.

Учитывая, что 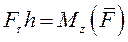-момент силы относительно оси Oz, получаем

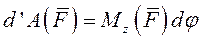
Работа силы в общем случае движения свободного твёрдого тела

Элементарная работа силы, приложенной в какой-либо точке твёрдого тела, в общем случае его движения равна сумме элементарных работ на элементарном поступательном перемещении вместе с полюсом и элементарном вращательном перемещении вокруг мгновенной оси, проходящей через полюс.

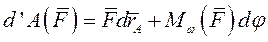
Скорость точки М приложения сила 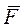в рассматриваемом случае

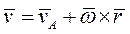
Где 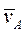- скорость полюса А; 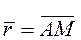. Тогда

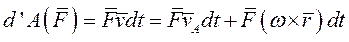
Так как

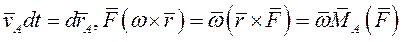
то

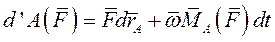
или

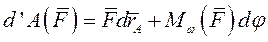
где 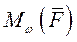- проекция 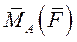на вектор 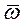; 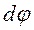-элементарный угол поворота тела вокруг мгновенной оси относительного вращения.