Элементарная и полная работа силы. Мощность. Работа равнодействующей силы.
Элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.
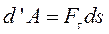
|
Элементарная работа силы равна скалярному произведению векторов силы и дифференциала радиус-вектора точки её приложения.
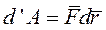 (I) (I)
|
Элементарная работа силы равна скалярному произведению элементарного импульса на скорость точки её приложения.
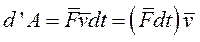
|
Пусть точка приложения силы 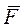 перемещается по криволинейной траектории из положения
перемещается по криволинейной траектории из положения 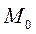 в положение
в положение 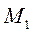 . Разобьём перемещение точки М по дуге
. Разобьём перемещение точки М по дуге 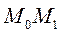 на элементарные бесконечно малые перемещения ds и определим работу силы на каждом таком перемещении
на элементарные бесконечно малые перемещения ds и определим работу силы на каждом таком перемещении
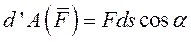
где 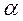 - угол между векторами
- угол между векторами 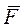 и
и 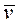 в точке
в точке 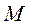 .
.
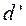 - выражение элементарной работы не всегда является полным дифференциалом.
- выражение элементарной работы не всегда является полным дифференциалом.
Т.к. 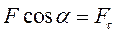 ,то
,то
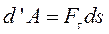
Поскольку 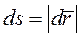
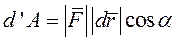 или
или 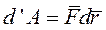
Так как 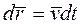
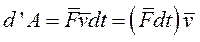
Можно представить (I) в виде
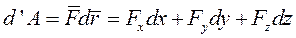
Полную работу силы 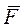 на перемещении точки из положения
на перемещении точки из положения 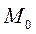 в положение
в положение 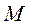 определяют как предел суммы её элементарных работ, т.е.
определяют как предел суммы её элементарных работ, т.е.
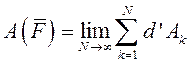
Так как сумма является интегральной суммой определения криволинейного интеграла, то
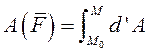
Или

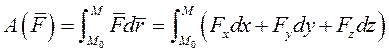
Если же сила является функцией времени (переменная сила) то работа силы 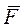 на промежутке времени от 0 до t, соответствующем точкам
на промежутке времени от 0 до t, соответствующем точкам 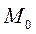 и
и 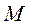 , определяется выражением
, определяется выражением
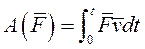
Работа силы зависит от характера движения точки приложения силы. Так, А = 0, если сила приложена к неподвижной точке или к точке, скорость которой во время движения равна нулю (например, МЦС)
Работа равнодействующей силы.
Рассмотрим систему сил, приложенную к рассматриваемой точке. Эта система имеет равнодействующую 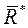 , причём
, причём
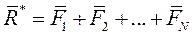
Тогда работа силы 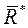 на перемещении точки из
на перемещении точки из 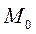 в текущее положение М равна алгебраической сумме работ составляющих сил на том же перемещении:
в текущее положение М равна алгебраической сумме работ составляющих сил на том же перемещении:
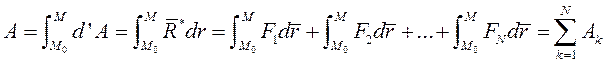
Мощнсть.
Отношение элементарной работы силы к промежутку времени, за которое оно произошло, называется мощностью.
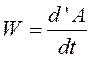
Так как 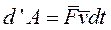 то
то
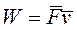
Мощность силы равна скалярному произведению силы на скорость точки её приложения.
Дата добавления: 2021-07-22; просмотров: 515;











