Теорема об изменении количества движения механической системы в дифференциальной и интегральной формах. Частные случаи.

Количеством движения материальной точки М называют вектор, равный произведению массы m точки на её скорость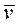

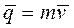
Количеством движения механической системы называют вектор 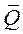, равный геометрической сумме количеств движения точек системы:

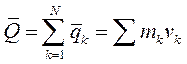
Вектор 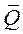называют также главным вектором количеств движения точек материальной системы.

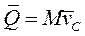
Элементарным импульсом силы 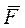, действующей в течении времени dt,

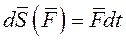
Теорема в дифференциальной форме.

Первая производная по времени от вектора количества движения механической системы равна главному вектору внешних сил, действующих на материальные точки этой системы.

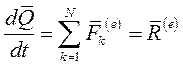
Запишем теорему о движении центра масс механической системы в виде

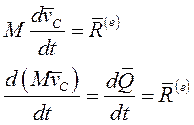
Окончательно имеем:

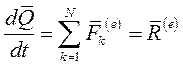(7)

Получим отсюда еще одну дифф. форму теоремы

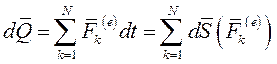(8)

Таким образом, дифференциал количества движения механической системы равен сумме элементарных импульсов внешних сил, действующих на материальные точки системы.

Теорема в интегральной форме

Изменение количества движения системы за время t равно векторной сумме полных импульсов внешних сил, действующих на точки механической системы за то же время.

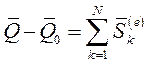
Проинтегрируем (8) по времени в пределах от 0 до t и поменяем местами операции интегрирования и суммирования:

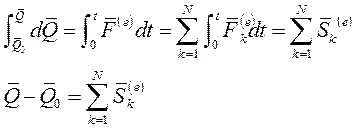
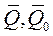- соответственно количества движения мех. системы в произвольный и начальный моменты времени. 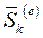- полный импульс внешней силы, действующей на k-ю материальную точку.