Кинетическая энергия точки и системы материальных точек. Теорема Кенига.

Кинетическую энергию материальной точки массой m, движущейся с абсолютной скоростью 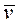, определяют по формуле

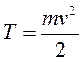
где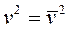

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек этой системы

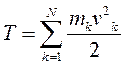
Теорема Кенига.

Кинетическая энергия механической системы в её абсолютном движении равна сумме кинетической энергии центра масс, в предположении, что в нём сосредоточена масса всей системы, и кинетической энергии движения системы относительно центра масс.

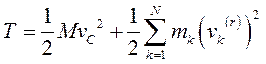
Рассмотрим движение механической системы в неподвижной системе отсчета Oxyz. В качестве подвижной выберем систему CXYZ с началом в центре масс, движущуюся поступательно вместе с центром масс. Абсолютное движение механической системы при этом можно рассматривать как совокупность переносного (вместе с ЦМ) и относительного (по отношению к ЦМ) движений системы.

Для любого момента времени положение произвольной точки 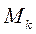по отношению к неподвижному центру О

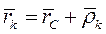
где 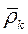- радиус-вектор точки 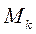по отношению к ЦМ. Продифференцируем и найдем абсолютную скорость:

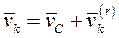
Учитывая, что квадрат вектора равен квадрату его модуля,

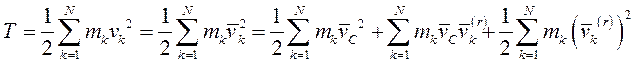
Здесь

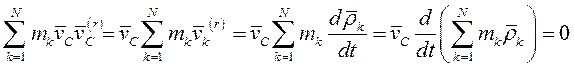
поскольку сумма статических моментов масс точек относительно центра масс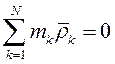

Таким образом

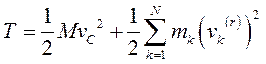
где 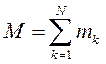- масса механической системы.