Центр масс системы материальных точек. Теорема о движении центра масс. Частные случаи.

Механическая система – совокупность материальных точек, положение или движение каждой из которых определяется положением или движением других точек этой совокупности.

Статический момент масс точек относительно к.л. центра О

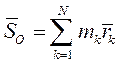
Момент инерции системы относительно центра О

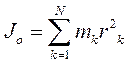
Статический момент массы мех. системы относительно к.л. точки О равен произведению массы системы 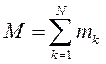на радиус-вектор центра масс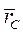

Откуда

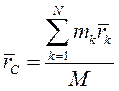(3)

Проецируем (3) на оси координат

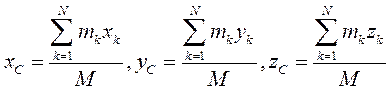
Выражения

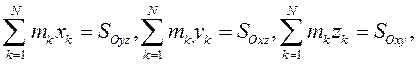
называют статическими моментами массы системы относительно координатных плоскостей. Отсюда имеем

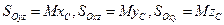
Теорема о движении центра масс

Центр масс механической системы движется как материальная точка, как бы обладающая массой системы, под действием системы всех внешних сил, действующих на точки системы.

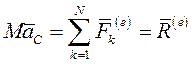
Запишем уравнения движения механической системы в виде

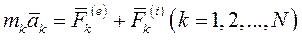(4)

Где 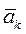-ускорение k-й точки, 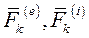- равнодействующие внешних и внутренних сил, действующих на k-ю точку.

Просуммируем уравнения (4) по всем точкам механической системы:

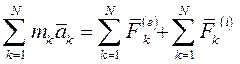
Здесь главный вектор внутренних сил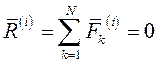

Дважды продифференцируем по времени (3)

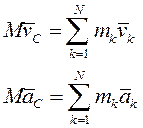
где 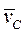- абсолютная скорость центра масс системы. Т.о.

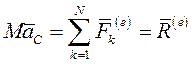(5)

Где 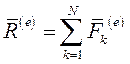- главный вектор сил, действующих на механическую систему.

В проекциях на координатные оси:

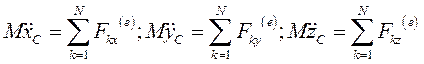(6)

Следствия.

1. Если главный вектор внешних сил, действующих на точки мех. системы, равен нулю, то центр масс мех. системы движется прямолинейно и равномерно.

Если главный вектор внешних сих, действ. на систему равен нулю, то из (5) следует, что 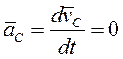, откуда после интегрирования получаем

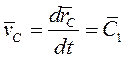
Интегрируя, получаем

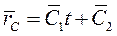
Постоянные 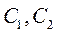определяем из начальных условий: при 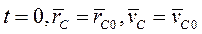. Для текущего момента времени при 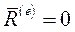окончательно имеем

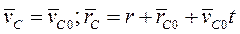
Если 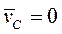, т.е. центр масс в начальный момент времени находится в покое, то

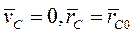
т.е. центр масс покоится в течение всего времени движения системы при условии, что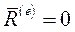

***

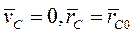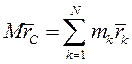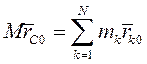Воспользуемся этим условием ( ) и запишем для текущего и начального положений мех. системы и . Вычитая из первого выражения второе, получаем

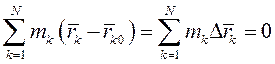
Следовательно, отдельные точки системы могут перемещаться при 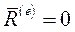и покоящемся центре масс.

***

2. Пусть теперь проекция главного вектора внешних сил, действующих на систему, на одну из осей (например, ось Ох) равна нулю 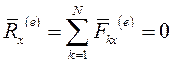, тогда из первого уравнения (6) следует 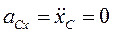, а значит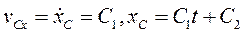

Постоянные определяем из начальных условий: при

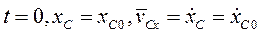. Для любого момента времени при 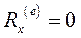окончательно имеем

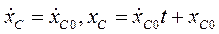
Если 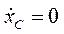т.е. проекция скорости центра масс на ось Ох в начальный момент времени равна нулю, то

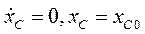
в любой момент времени.

***

Воспользуемся 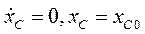и, согласно (6) напишем для текущего и начального моментов времени

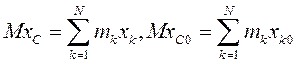
Вычитая из первого уравнения второе, получим

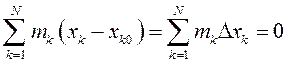
Из уравнения следует, что перемещение k-й точки 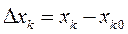вдоль оси Ох существует при 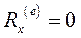и отсутствии перемещений вдоль этой оси центра масс