Две основные задачи динамики точки. Интегралы уравнений движения.
Первая задача состоит в том, чтобы по заданному закону движения точки массой m определить силу, под действием которой происходит это движение.
Вторая задача состоит в определении движения точки по заданным силам и начальным условиям движения, при этом силы должны быть выражены как функции переменных, используемых для задания движения.
Решение этой задачи сводится к интегрированию диф. уравнений второго порядка, в процессе которого в решениях появляются произвольные постоянные.
В задаче о движении точки в трехмерном пространстве общие решения будут содержать шесть произвольных постоянных:
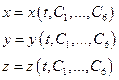
Если начальные условия поставлены для начальных значений функций и их первых производных, т.е. в виде
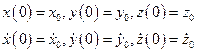
то задача Коши имеет единственное решение. Т.о. приложенные к точке силы определяют только её ускорение, движение же точки помимо сил зависит от начальных условий – положения точки в рассматриваемой инерциальной системы отсчета и её скорости.
Первым интегралом системы дифференциальных уравнений (1) называется функция
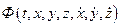
Выражение
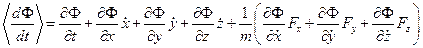
называется производной по времени функции 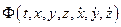 , вычисленной в силу дифференциальных уравнений (1).
, вычисленной в силу дифференциальных уравнений (1).
Для того чтобы полностью найти закон движения материальной точки, достаточно найти шесть функционально независимых первых интегралов.
Пусть
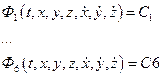
- шесть независимых первых интегралов системы (1).
Т.к. по условию 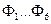 - функционально независимы получаем общее решение системы:
- функционально независимы получаем общее решение системы:
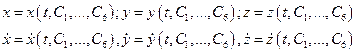
Дата добавления: 2021-07-22; просмотров: 834;











