Дифференциальные уравнения движения точки в векторной форме и в проекциях на декартовы и естественные оси координат.
Аксимомы динамики. Инерциальная система отсчета.
- Существуют системы отсчета, называемые инерциальными, по отношению к которым материальная точка, не испытывающая действия или находящаяся вод действием уравновешенной системы сил, сохраняет состояние покоя или равномерного прямолинейного движения.
- Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силы и совпадает с ней по направлению.
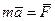
- Силы взаимодействия двух материальных точек направлены по прямой, соединяющей эти точки, в противоположные стороны и равны по модулю
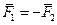
- Ускорение, полученное точкой под действием системы сил, равно векторной сумме ускорений от действия отдельных сил
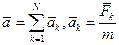
Дифференциальные уравнения движения точки в векторной форме и в проекциях на декартовы и естественные оси координат.
Из второй и четвёртой аксиом следует уравнение движения в инерциальной системы отсчёта:
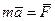
Где F – равнодействующая всех сил, приложенных к точке.
Векторное дифф. уравнение движения точки:
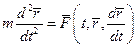
Диф. уравнения в проекциях на декартовы оси:
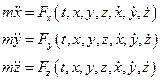 (1)
(1)
В проекциях на естественные оси:
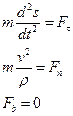
Дата добавления: 2021-07-22; просмотров: 590;











