Уравнение состояния
Параметры состояния термодинамической системы связаны между собой зависимостью, которая называется уравнением состояния. Это уравнение устанавливает функциональную зависимость параметров состояния f(р,T,v)=0. С математической точки зрения функция f(р,T,v)=0 в трехмерном пространстве описывает конкретную поверхность, каждая точка на которой отображает равновесные состояния ТДС. Эта поверхность называется термодинамической поверхностью. Уравнение состояния позволяет символично выразить каждый из параметров через два других параметра, т.е.
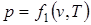 ;
; 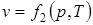 ;
; 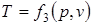 .
.
Следует отметить, что современная физика пока не располагает универсальным уравнением состояния для всех форм материальных тел. На сей день имеется ряд эмпирически установленных зависимостей для некоторых категорий материальных тел, описывающих их термодинамическое состояние.
Для идеального газа эта зависимость называется уравнением Клапейрона-Менделеева и имеет вид:
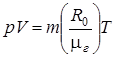 , (1.3)
, (1.3)
где р – давление, (Па); V – объем газа, (м3); m – масса газа, (кг); R0=8314 ( 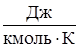 ) - универсальная газовая постоянная,
) - универсальная газовая постоянная, 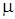 г – мольная масса газа, (
г – мольная масса газа, ( 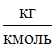 ); Т – абсолютная температура, (К).
); Т – абсолютная температура, (К).
Путем введения понятия удельного объема 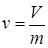 , то уравнение (1.3) можно написать в виде
, то уравнение (1.3) можно написать в виде
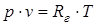 , (1.4)
, (1.4)
где 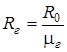 , (
, ( 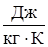 ),- удельная газовая постоянная, характеризует физические свойства конкретного газа. Для некоторых газов их свойства представлены в табл. 1.1.
),- удельная газовая постоянная, характеризует физические свойства конкретного газа. Для некоторых газов их свойства представлены в табл. 1.1.
Таблица 1.1
| Газ | μ, кг/кмоль | R, Дж/(кг К) | ρ0, кг/м3 |
| Водород Н2 | 0,09 | ||
| Гелий Не | 0,18 | ||
| Азот N2 | 1,25 | ||
| Кислород О2 | 1,43 | ||
| Воздух | 29,1 | 1,29 | |
| Углекислый газ СО2 | 1,81 | ||
| Водяной пар Н2О | 0,71 |
Для реальных газов, в которых необходимо учитывать межмолекулярные силы взаимодействия и нельзя пренебрегать объемами молекул. Соответствующее уравнение состояния было предложено Ван-дер-Ваальсом, которое имеет вид
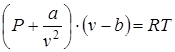 , (1.5)
, (1.5)
где а – учитывает силу взаимодействия молекул, b – представляет собой суммарный объем молекул.
Теплоемкость
Теплоемкостью С называют отношение подведенного к телу количества теплоты ΔQ к достигнутой при этом разности температур тела ΔT:
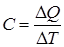 . (1.6)
. (1.6)
Отношение теплоемкости тела к его массе m есть удельная теплоемкость
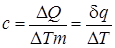 . (1.7)
. (1.7)
Произведя предельный переход в последнем выражении, приходим к формуле
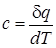 , (1.8)
, (1.8)
которая позволяет определить истинную теплоемкость.
Дата добавления: 2021-07-22; просмотров: 556;











