Законы идеального газа

Основные законы термодинамики. Термодинамика идеального газа

Раздел содержит три темы, три лабораторные и одну контрольную работы (задачи № 1,2,3,4), вопросы для самопроверки и контрольный тест из десяти вопросов (№ 1). Максимально возможное число баллов по этому разделу составит 55 баллов для очно-заочной и заочной формам обучения.

Термодинамика идеального газа

Уравнение состояния идеального газа. Универсальная газовая постоянная. Удельная газовая постоянная. Нормальные физические условия. Молекулярно – кинетическая теория теплоемкости. Элементы квантовой теории теплоемкости. Истинная и средняя теплоемкости. Свойства теплоемкостей идеального газа. Связь между изохорной и изобарной теплоемкостями идеального газа (закон Майера). Эмпирические формулы для теплоемкостей идеального газа. Таблицы значений истинной и средней теплоемкостей идеального газа.

Cмеси идеальных газов. Закон Дальтона. Теплоемкость газовых смесей.

По теме выполняются практические занятия (№ 1), две лабораторные работы (№ 1,2), контрольная работа (задачи № 1,2,3). После изучения теоретического материала следует ответить на вопросы для самопроверки по этой теме. Ответы можно найти в учебниках [1,3].

Основные понятия и определения термодинамики.

Прежде чем приступить к подробному изучению курса технической термодинамики следует ознакомиться с основными понятиями и определениями данной дисциплины.

1. Термодинамической системой (ТДС) называется совокупность тел, выделенная из окружающей среды (ОС) воображаемой или реальной поверхностью, через которую между ТДС и ОС может осуществляться обмен энергией 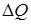и веществом .

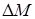Известны три категории ТДС:

а) при условиях , - ТДС называется открытой;

б) при , 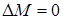- ТДС – закрытая;

в) при 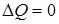, 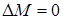- ТДС изолирования.

2. В термодинамике простейшую ТДС называют рабочим телом (РТ). Рабочее тело является необходимым посредником, способным воспринимать теплоту (холод) и совершать работу. В свою очередь РТ делится на две категории:

а) Идеальный газ – это материя, объемами микрочастиц которой и их взаимодействием между собой можно пренебречь (примеры: низкомолекулярные газы – водород, кислород, воздух, перегретый водяной пар и др.).

б) Реальные газы – это материя, микрочастицы которой обладают конечными объемами и между собой дистанционно взаимодействуют (пример – высокомолекулярные углеводороды и др.).

3. Термодинамическое состояние ТДС, которое характеризуется всеми свойствами системы. Вообще состояние ТДС определяется ограниченным числом величин, называемых параметрами состояния. В газах и жидкостях при отсутствии химических реакций параметрами состояния являются:

температура – Т, К; давление – р, Па; удельный объем – v, .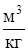

Температура – это мера интенсивности беспорядочного теплового движения молекул. Абсолютная температура Т связана со средней скоростью молекул w соотношением

,

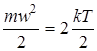где k = 1,381·10^-23 – постоянная Больцмана, m – масса молекулы. Единица измерения абсолютной температуры – Кельвин (К). Ноль шкалы Кельвина соответствует полному покою молекул. Практически широко применяется шкала Цельсия. Градус Цельсия равен градусу Кельвина; 0°С соответствует 273,15 К.

Давление p – это сила, действующая со стороны газа или жидкости на единицу площади стенки по нормали к ней. Давление измеряется в паскалях Па, 1 Па = 1 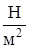. 1 килопаскаль равен 10³ Па, 1 мегапаскаль – это 10⁶ Па. Среднее атмосферное давление р₀=1,013·10⁵ Па≈0,1 МПа. Устаревшая единица давления – техническая атмосфера (ат). 1 ат = 0,98·10⁵ Па≈0,1 МПа. Параметром состояния является полное (абсолютное) давление. Манометром измеряется давление, избыточное над атмосферным, р_изб = р – р₀.

Удельный объем v – это объем единицы массы рабочего тела (вещества). Если объем газа V и масса m, то v= 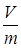, 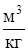. Удельный объем связан с плотностью газа 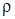соотношением v = .

Нормальные термодинамические параметры воздуха:

Т₀ = 273,15 К; р₀ = 101,3·10³ кПа; v₀ = 0,770 .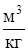

4. Под термодинамическим процессом понимается совокупность последовательных состояний, через которую проходит ТДС при её взаимодействии с окружающей средой. Состояние ТДС может быть равновесным и неравновесным. Равновесным называется такое состояние ТДС, при котором во всех точках её объема все параметры состояния и физические свойства одинаковы. В противном случае ТДС называют неравновесным.

Все процессы, проходящие в ТДС, подразделяются на равновесные и неравновесные. Равновесными называются такие процессы, когда ТДС в ходе процесса проходит ряд последовательных равновесных состояний. Эти процессы протекают настолько медленно, что в каждый момент времени устанавливается равновесие.

Неравновесными называются такие процессы, при протекании которых ТДС не находится в состоянии равновесия.

Наряду с понятиями равновесности и неравновесности в термодинамике используют понятия обратимости и необратимости. Обратимость процесса состоит в том, что он может протекать и в прямом (например, расширение) и обратном (сжатие) направлениях так, что при этом и окружающая среда и ТДС проходят одни и те же состояния. Обратимый процесс в обратном направлении восстанавливает первоначальное состояние ТДС и ОС.

Необратимый процесс в прямом направлении проходит через одни состояния, в обратном – через другие, и в обратном направлении не восстанавливает первоначальное состояние ТДС и ОС. Чем медленнее развиваются процессы, тем меньше влияние необратимости. Процесс может быть обратимым при условии, если его время осуществления стремится к бесконечности.

Все реальные процессы, протекающие в природе, являются неравновесными. По этой причине эти процессы лишь с той или иной степенью точности могут описываться закономерностями, справедливыми для равновесных процессов.

В термодинамике в первую очередь рассматриваются равновесные процессы и равновесные состояния, которые могут быть количественно описаны соответствующими уравнениями термодинамики.

5. Внутренняя энергия U – это энергия, заключенная в рассматриваемой ТДС, которая представляет собой сумму кинетической энергии хаотичного движения микрочастиц системы. Внутренняя энергия является функцией параметров состояния, т.е. её изменение не зависит от формы пути процесса, а определяется лишь её значениями в конечном и начальном состояниях, т.е.

.

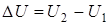Обозначив массу рассматриваемой ТДС через m (кг) и поделив внутреннюю энергию системы U на её массу, можно получить выражение для энергии, приходящейся на единицу массы, которая называется удельной внутренней энергией

.

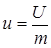6. Теплота и работа. Обмен энергией между ТДС и ОС может осуществляться в двух различных формах – в форме теплоты и в форме механической работы.

Теплота представляет собой микроскопическую форму обмена энергией между ТДС и ОС. В этом случае обмен происходит без изменения формы и объема ТДС, при этом меняются лишь значения давления и температуры в системе. Пример – подвод теплоты 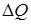извне (например – пламенем паяльной лампы) в газ, находящийся в замкнутой металлической емкости. В этом случае по мере подвода теплоты наблюдается рост температуры и давление газа, следовательно, происходит увеличение внутренней энергии газа U при неизменном объеме. Таким образом, в данном примере осуществляется обмен энергией между окружающей средой (паяльной лампой) и газом, находящимся внутри емкости.

Механическая работа – это макроскопическая форма обмена энергией между ТДС и ОС. В этом процессе происходит изменение значений всех параметров состояния. В результате изменения (расширения) объема ТДС совершается механическая работа по преодолению сопротивления окружающей среды. Из механики известно, что работа равна произведению силы на пройденный путь в направлении действия данной силы. Величина этой работы пропорциональна давлению газа р и приращению объема 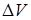при расширении. Пример – нагрев извне газа (например, пламенем той же паяльной лампы), находящегося в вертикальном цилиндре с подвижным поршнем. В этом случае подвод теплоты из ОС обусловливает рост температуры и давления газа внутри емкости (в ТДС), что сопровождается подъемом поршня вверх в результате расширения газа. При этом совершается механическая работа по преодолению силы тяжести поршня. Обозначив эту работу через , её можно выразить в виде следующей зависимости = F·Dh, где F=p·f - сила давления газа на поршень, f - площадь поперечного сечения поршня, Dh-высота подъема поршня в результате расширения газа. Учитывая, что f·Dh=DV - приращение объема газа внутри цилиндра, выражение для работы можно представить в виде

.

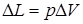Производя предельный переход в последнем выражении, его можно представить в дифференциальной форме

.

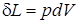Это уравнение выражает элементарную термодинамическую работу расширения ТДС. Соответствующую удельную работу, т.е. отнесенную к 1 кг газа, можно представить уравнением

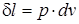. (1.1)

7. Функцией состояния ТДС называется такая физическая характеристика системы, изменение которой при переходе системы из одного состояния в другое не зависит от вида соответствующего этому переходу термодинамического процесса и определяется значениями параметров начального и конечного состояния.

(Как было отмечено выше, теплота Q и работа L представляют собой различные формы обмена внутренней энергией между ТДС и ОС. Для этих двух функций их бесконечно малое приращение в термодинамике принято обозначать оператором « 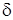», в отличие от дифференциала функций состояния, которые обозначаются оператором «d»).

Функциями состояния являются, прежде всего, известные нам параметры состояния р, v, T и внутренняя энергия U. Рассмотрим еще несколько функций состояния, имеющих широкое распространение.

8. Энтальпия. Наряду с внутренней энергией U в термодинамике важную роль играет величина, называемая энтальпией

.

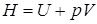где первое слагаемое в правой части, как известно, представляет сумму кинетической энергии микрочастиц системы, второе слагаемое – потенциальную энергию взаимодействия микрочастиц системы, следовательно, левая часть составляет полную энергию.

Удельная энтальпия h = 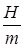выражается зависимостью:

.

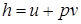9. Энтропией называется функция состояния S, дифференциал которой для элементарного термодинамического процесса равен отношению бесконечно малого количества теплоты 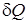сообщаемого системе, к абсолютной температуре последней

.

Энтропия может быть определена только с точностью до аддитивной произвольной постоянной

,

S₀ –константа интегрирования.

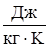Удельная энтропия - имеет размерность ( ). Выразим основное соотношение, используя понятие удельной энтропии:

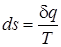или 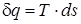. (1.2)

Введение данной функции состояния значительно облегчает анализ термодинамических процессов. Физическая сущность энтропии – есть мера необратимого рассеяния энергии.

Законы идеального газа

При теоретическом изучении термодинамического состояния идеального газа используется ряд физических законов:

1. Закон Бойля-Мариотта – произведение абсолютного давления газа на его удельный объем, при T=const, есть величина постоянная (рv=const).

Таким образом, для двух последовательных состояний газа согласно этому закону, имеем:

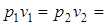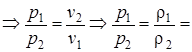const const

2. Закон Гей-Люссака – отношение удельного объема газа, при р=const, к абсолютной температуре есть величина постоянная ( 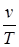=const).

Тогда для двух последовательных состояний газа имеем:

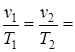const, , .

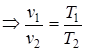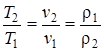3. Закон Шарля - при v=const отношение температуры к давлению есть величина постоянная ( 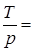const). Для двух последовательных состояний имеем:

.

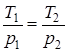4. Закон Авогадро – при одинаковых давлениях и температурах в равных объемах различных идеальных газов содержится одинаковое число молекул, что то же самое при одинаковых давлениях и температурах один моль различных газов занимает одинаковый объем. При нормальных физических условиях по закону Авогадро объем одного киломоля идеального газа составляет V_м=22,4м³.