Первый закон термодинамики

Термодинамическая система и окружающая среда. Изолированная и неизолированная термодинамические системы. Параметры состояния. Уравнение состояния. Термодинамическая поверхность. Термодинамический процесс. Равновесные и неравновесные процессы (взаимодействие). Теплота и работа как функции процесса. Внутренняя энергия и энтальпия как функции состояния термодинамической системы (рабочего тела).

Свойства внутренней энергии и энтальпии идеального газа. Энтропия как функция состояния. Таблицы термодинамических свойств идеальных газов. Изохорный, изобарный, изотермический и адиабатный процессы с идеальным газом. Политропные процессы и их анализ. Расчет количества теплоты и изменения температуры по таблицам значений энтальпии и внутренней энергии идеального газа.

Закон сохранения и превращения энергии. Первый закон термодинамики. Различные аналитические выражения первого закона термодинамики. Краткая история открытия первого закона термодинамики.

По теме выполняется одна лабораторная работа (№ 3), контрольная работа (задача № 4). После изучения теоретического материала следует ответить на вопросы для самопроверки по этой теме. Ответы также можно найти в учебниках [1,3].

Первый закон термодинамики установлен экспериментально на основании многовекового опыта человечества. Все процессы, происходящие в природе, протекают при строгом соблюдении этого закона.

Если к рабочему телу с массой m подводится теплота δQ, то при этом происходит, в общем случае, приращение внутренней энергии ΔU (рост температуры и давления) и совершается работа расширения δL против сил окружающей среды. Применительно к этому процессу можно записать зависимость, выражающую универсальный закон сохранения и превращения энергии:

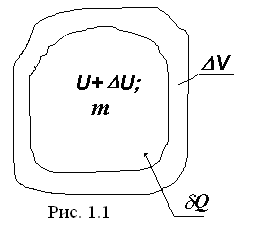
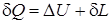. (1.25)

Поделив обе части последнего уравнения на массу рабочего тела m и далее произведя предельный переход, получим следующую зависимость

, (1.26)

которая является математической записью первого закона термодинамики.

В литературе часто используются два варианта записи этого уравнения. В частности, используя формулу для элементарной работы расширения (1.1), выражение ( 1.26 ) можно представить в виде

δq=du+p∙dv. (1.27)

Преобразуя второе слагаемое в правой части последнего уравнения

pdv = d(pv) –vdp,

подставив его в (1.27) получим следующую форму записи первого закона термодинамики

δq=dh-v∙dp. (1.28)

Проанализируем некоторые характерные термодинамические процессы с помощью первого закона термодинамики.

а). Процесс протекает при постоянном удельном объеме (v=const., dv=0).

Из уравнения (1.27) при v=const, dv=0 следует

δq=du.

Последнее выражение рассматриваем совместно с формулой (1.9)

δq=du;

δq=сdT.

В силу равенства левых частей этих выражений, приравниваем их правые части и учитывая что, при v=const, c=с_v, окончательно имеем

du = с_vdT. (1.29)

б). Термодинамический процесс протекает при постоянном давлении (p=const, dp=0). Для этого случая из (1.28) следует

δq=dh.

Рассматривая это выражение совместно с формулой (1.9), получаем систему уравнений

δq=dh,

δq=сdT.

Приравнивая правые части этих выражений, учитывая так же, что теплоемкость данного процесса с=с_р, приходим к следующей зависимости

dh= с_pdT. (1.30)

В термодинамике идеального газа формулы (1.29 и 1.30), наряду с выражением для элементарной работы δl=pdv (1.1), играют фундаментальную роль при анализе различных процессов.