Смеси идеальных газов

Если в замкнутый объем поместить несколько между собой химически инертных газов, то в результате их механического перемешивания образуется субстанция с новыми термодинамическими свойствами, которая называется газовой смесью.

Если обозначить массу, объем и давление газовой смеси соответственно m_см, V_см и p_см, то эти параметры можно выразить через соответствующие параметры компонентов, составляющих эту смесь:

m_см= m₁+ m₂+…+m_n =åm_i - масса смеси;

V_см= V₁+V₂+…+V_n =åV_i - объем смеси;

p_см=p₁+p₂+…+p_n=åp_i - давление смеси, (закон Дальтона)

В вышеприведенных формулах суммирование ведется в пределах: i=1,2…n, где n- число компонентов, из которых состоит газовая смесь;

m_i – масса i-го компонента; V_i, p_i – приведенный объем и парциальное давление i^го компонента смеси.

В термодинамике применяются следующие понятия:

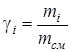- массовая доля i-го компонента;

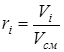- объемная доля i-го компонента.

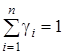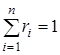Очевидна правомерность следующих равенств: и , где суммирование ведется по i=1, 2…n.

Мольная (кажущаяся) масса смеси определяется по одной из следующих формул

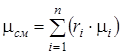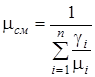; . (1.17)

Газовая постоянная смеси определяется по следующим формулам:

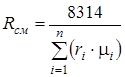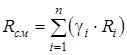; , (1.18)

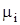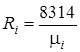где и - соответственно мольная масса и газовая постоянная i-го компонента смеси.

Смесь количественно может быть задана в массовых g_i и объемных r_i долях. Связь между g_i и r_i выражается при помощи следующих формул:

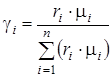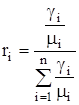, . (1.19)

В смеси, находящейся в термодинамическом равновесии, температура в пределах всего объема V_см всюду одинакова, обозначим ее T_см. Если все компоненты газовой смеси соответствуют определению идеального газа, то термодинамическое состояние этой смеси описывается уравнением Клапейрона-Менделеева:

p_см×V_см=m_см×R_см×T_см. (1.20)

При тепловых расчетах часто приходится иметь дело со смесями газов. В подобных случаях возникает необходимость определения теплоемкости смеси. В термодинамических таблицах приводятся только теплоемкости отдельных компонентов смеси.

Существуют формулы, позволяющие определять эти величины. В зависимости от того, как задана смесь, удельную теплоемкость смеси можно рассчитывать при помощи формул:

смесь задана массовыми долями :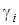

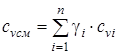- изохорная массовая удельная теплоемкость смеси; (1.21)

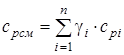- изобарная массовая удельная теплоемкость смеси; (1.22)

в случае задания смеси в объемных долях :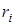

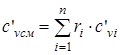- изохорная объемная удельная теплоемкость смеси; (1.23)

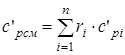- изобарная объемная удельная теплоемкость смеси, (1.24)

где соответственно обозначают 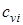, , 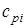и 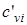, 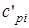- массовые изохорная, изобарная и объемные изохорная, изобарная теплоемкости i-го компонента смеси, значения которых приведены в специальных таблицах в [9].

Вопросы для самопроверки

1. Какой газ называется идеальным?

2. Что такое нормальные физические условия? Какой объем занимает киломоль любого газа при нормальных физических условиях?

3. В чем сущность молекулярно-кинетический теории теплоемкости? Каковы основные недостатки этой теории?

4. В чем сущность квантовой теории теплоемкости? Какие преимущества имеет эта теория перед молекулярно-кинетической теории теплоемкости?

5. Какова связь между истинной и средней теплоемкостями? Как вычислить теплоту процесса с помощью каждой из этих теплоемкостей?

6. Какими свойствами обладают теплоемкости идеального газа?

7. Как связаны изобарная и изохорная теплоемкости идеального газа?

8. В какой форме может быть задана зависимость теплоемкости идеального газа от температуры?

9. Какими способами может быть задана смесь идеальных газов?

10. Что такое кажущаяся мольная масса смеси идеальных газов?

11. Сформулируйте закон Дальтона. В каком случае справедлив этот закон?

12. Что такое парциальное давление и парциальный (приведенный) объем?

13. Как рассчитывается теплоемкость смеси идеальных газов при различных способах задания этой смеси?

14. Получите выражение для определения удельной газовой постоянной смеси идеальных газов.