Понятие и свойства точечных оценок

Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки, которую можно сформулировать следующим образом.

Пусть распределение признака Х – генеральной совокпности – задается функцией вероятностей 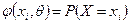(для дискретной случайной величины Х) или плотностью вероятности 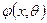(для непрерывной случайной величины Х), которая содержит неизвестный параметр 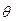. Для вычисления данного параметра исследовать все элементы генеральной совокупности не представляется возможным. В связи с этим о параметре 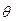пытаются судить по выборке (x₁, x₂, …, x_n). Данные значения можно рассматривать как частные значения (реализации) n независимых случайных величин Х₁, Х₂, …, Х_n, каждая из которых имеет тот же закон распределения, что и сама случайная величина Х.

Точечной оценкой 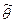параметра 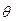называют функцию результатов наблюдений над случайной величиной Х, подсчитанное значение которой принимается за 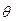, т.е.

.

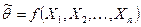Основными методами нахождения оценок являются метод моментов, метод максимального правдоподобия, метод наименьших квадратов.

Точечные оценки могут обладать свойствами несмещенности, состоятельности и эффективности.

Несмещенной называют статистическую оценку 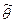, математическое ожидание которой равно оцениваемому параметру 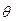при любом объеме выборки, т.е.

.

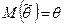Смещенной называют статистическую оценку, математическое ожидание которой не равно оцениваемому параметру.

В теории математической статистики доказано, что 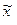- является несмещенной оценкой, а 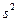- смещенной, т.е.

,

,

.

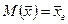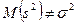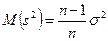В связи с тем, что практический смысл имеют несмещенные оценки, поэтому в расчетах используют исправленную выборочную дисперсию, являющуюся несмещенной оценкой, т.е.

,

.

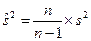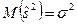Несмещенную оценку 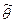параметра 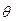называют эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 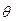, вычисленных по выборкам одного и того же объема n.

К примеру, на практике в целях упрощения расчетов генеральную среднюю 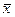часто оценивают медианой выборки, в то время как эффективной оценкой 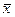является выборочная средняя .

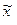Оценку 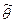параметра 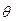называют состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е.

.

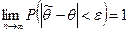К примеру, в теории математической статистики доказано, что выборочная дисперсия является состоятельной оценкой, т.е.

.

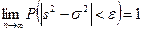В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.