Моменты распределения. Асимметрия и эксцесс

Для подробного описания особенностей распределения используют дополнительные характеристики – моментыраспределения, предложенные П.Л. Чебышёвым.

Моментом m-го порядка называют среднюю из m-х степеней отклонений вариантов х от некоторой постоянной величины A:

.

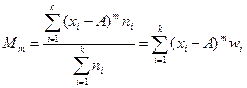При A=0 получают начальные моменты, при 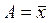– центральные моменты, а если A – какая-либо другая постоянная величина, то получают условные моменты (начальные моменты относительно A).

Начальным моментом m-го порядка называют величину:

.

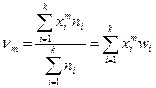Исходя из формулы начального момента: , .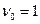

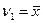Центральным моментом m-го порядка называют величину:

.

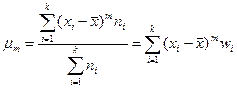Можно показать, что , , .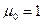

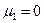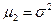Центральный момент третьего порядка используется при исчислении показателя асимметрии распределения. Для того чтобы показатель асимметрии не зависел от масштаба, выбранного при измерении вариантов, вводят безразмерную характеристику – коэффициент асимметрии (нормированный момент третьего порядка):

.

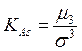Если K_As = 0, то распределение симметричное (в симметричных распределениях средняя, мода и медиана совпадают). При K_As > 0 – левосторонняя асимметрия, а при K_As < 0 – правосторонняя.

Рис. __. Асимметрия распределения

В качестве показателя асимметрии применяется также коэффициент асимметрии Пирсона:

.

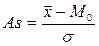Если As > 0, то распределение имеет правостороннюю асимметрию, если As < 0 – левостороннюю, при As = 0 – распределение симметрично.

Для характеристики крутизны распределения используется эксцесс распределения (нормированный момент четвертого порядка минус три):

.

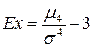Для нормального симметричного распределения Ex = 0 (данное распределение используется в качестве эталона).

Рис. __. Эксцесс распределения