Сущность интервального оценивания

Между характеристиками генеральной и выборочной совокупности, как было отмечено выше, возможно расхождение, т.е. наличие ошибки репрезентативности, подразделяющейся на систематическую и случайную составляющие. Оценка таких ошибок – одна из задач статистики, для решения которой используют интервальное оценивание, позволяющее получить представление о точности и надежности оценки.

Интервальной оценкой параметра 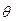называется числовой интервал 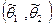, который с заданной вероятностью 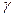накрывает неизвестное значение параметра 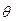(рисунок 2).

Рисунок 4. Интервальная оценка параметра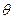

Интервал 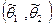- называют доверительным, а вероятность 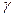- доверительнойвероятностью (уровнем доверия, надежностью оценки).

Величина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вероятности 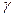(увеличивается с приближением 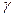к единице).

Зачастую, доверительный интервал выбирается симметричным относительно параметра 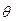, т.е. .

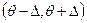Наибольшее отклонение 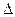оценки 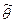от оцениваемого параметра 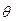, которое возможно с заданной доверительной вероятностью 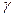, называют предельной ошибкой выборки (случайной ошибкой репрезентативности), т.е.

.

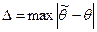Выборка считается репрезентативной, если относительное значение предельной ошибки выборки не превышает, как правило, 5% от значения оцениваемого параметра, т.е.

.

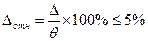Наряду с предельной ошибкой выборки выделяют среднююквадратическую (стандартную) ошибкувыборки, т.е. среднее квадратическое отклонение всех возможных значений оценки от оцениваемого параметра. К примеру, формулы для расчета стандартной ошибки выборки при оценке параметров 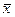и p для различных видов выборок и методов отбора приведены в таблице 2.

Предельную ошибку выборки определяют в долях средней квадратической ошибки с заданной вероятностью, т.е.

,

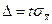для доли

,

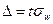где t – коэффициент доверия (надежности), зависящий от вероятности, с которой определяется предельная ошибка выборки.[6]

Александр Михайлович Ляпунов доказал, что независимо от характера распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению. Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчинена указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа (приложение 1), т.е.

,

.

,

.

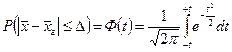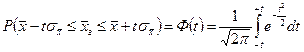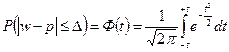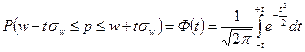Таблица 10

Формулы расчета стандартной ошибки выборки[7]

№	Тип выборки	Оцениваемый параметр	Повторный отбор	Бесповторный или механический отбор
1.	Собственно-случайная и механическая выборка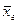
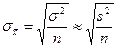
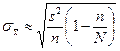
p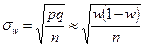
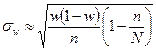
2.	Типическая (стратифицированная) выборка	при отборе, пропорциональном объему типических групп
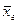
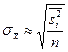
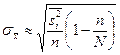
p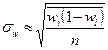
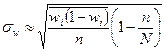
при отборе, пропорциональном вариации признака в типических группах
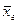
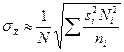
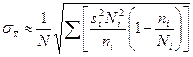
p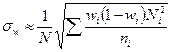
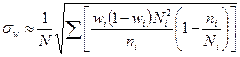
3.	Серийная (гнездовая) выборка[8]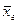
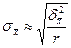
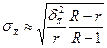
p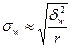

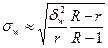
Примечания:

1) N_i, n_i - объем i-ой типической группы в генеральной совокупности и в выборке соответственно

2) R, r – число серий в генеральной совокупности и в выборке соответственно.

3) 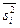- средняя из групповых выборочных дисперсий при оценке генеральной средней.

4) 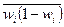- средняя из групповых выборочных дисперсий при оценке доли.

5) 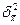, 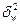- межсерийные выборочные дисперсии, к примеру, в случае равновеликих серий[9]

,

,

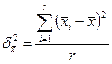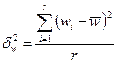где 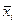, 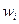- среднее значение признака в i-ой серии при оценке генеральной средней и доли соответственно, рассчитываемые по следующим формулам:

,

.

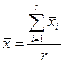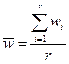6) Стандартная ошибка выборки при многоступенчатом отборе складывается из ошибок, возникающих на каждой ступени (этапе отбора). Например, в случае двухступенчатого отбора, если на первой ступени отбираются укрупненные единицы (серии), а затем без проведения обследования в рамках серии осуществляется собственно-случайный или механический отбор единиц из каждой отобранной серии формула для расчета стандартной ошибки выборочной средней примет следующий вид:

,

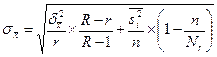где N_r – общее число единиц совокупности в отобранных сериях.