Оптимальное решение определяется следующим образом: базисные переменные приравниваются соответствующим правым частям, остальные нулю.
Пример. Решить ЗЛП:
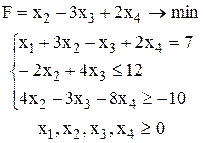
Приведем ЗЛП к канонической форме:
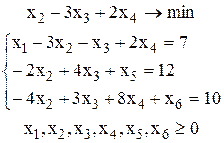
Базисные переменные: 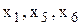
Составим симплекс-таблицу.
| xd | cd | b | -3 | |||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x1 | -1 | |||||||
| x5 | -2 | 4 | ||||||
| x6 | -4 | |||||||
| -1 | -2 |
Строка оценок вычисляется следующим образом:
D1 = 0 × 1 + 0 × 0 + 0 × 0 – 0 = 0
D2 = 0 × 3 + 0 × (-2) + 0 × (-4) – 1 = -1
D3 = 0 × (-1) + 0 × 4 + 0 × 3 + 3 = 3
D4 = 0 × 2 + 0 × 0 + 0 × 8 – 2 = -2
D5 = 0 × 0 + 0 × 1 + 0 × 0 – 0 = 0
D6 = 0 × 0 + 0 × 0 + 0 × 1 – 0 = 0
Исходный план X = (1; 0; 0; 0; 2; 5) не является оптимальным, т.к. в строке оценок имеется положительный элемент 3. Следовательно, третий столбец оценок выбирается в качестве ведущего, а переменная x3 на текущей операции станет базисной вместо переменной x5. Для определения ведущей строки выбираем в ведущем столбце положительные элементы, находим отношения правых частей соответствующих ограничений к данным элементам и из них выбираем минимальное. Для второй строки отношение 2/4 = 1/2. Для третьей строки отношение 5/3. Следовательно, в качестве ведущей выбирается вторая строка, а элемент 4 (в симплекс-таблице он выделен) становится ведущим.
Далее элементы симплекс-таблицы пересчитываются. Вся ведущая строка делится на ведущий элемент. Остальные элементы пересчитываются по правилу прямоугольника.
Рассмотрим в качестве примера пересчет элементов первой строки:
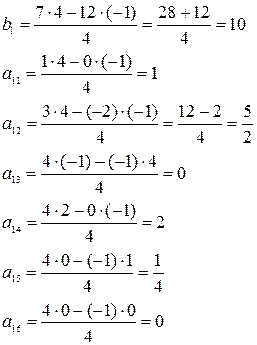
Остальные элементы пересчитываются аналогично. После пересчета получим следующую симплекс-таблицу:
| xd | cd | B | -3 | |||||
| x1 | X2 | x3 | x4 | x5 | x6 | |||
| x1 | 5/2 | 1/4 | ||||||
| x3 | -3 | -1/2 | 1/4 | |||||
| x6 | -5/2 | -3/4 | ||||||
| -9 | 1/2 | -2 | -3/4 |
Оценки считаются следующим образом:
D1 = 0 × 1 + (-3) × 0 + 0 × 0 – 0 = 0
D2 = 0 × 5/2 + (-3) × (-1/2) + 0 × (-5/2) – 1 = -1/2
D3 = 0 × 0 + (-3) × 1 + 0 × 0 + 3 = 0
D4 = 0 × 2 + (-3) × 0+ 0 × 8 – 2 = -2
D5 = 0 × 1/4 + (-3) × 1/4 + 0 × (-3/4) – 0 = -3/4
D6 = 0 × 0 + (-3) × 0 + 0 × 1 – 0 = 0
Оптимальное решение не получено, т.к. в строке оценок имеется положительный элемент.
В качестве ведущего столбца выбирается второй столбец, в качестве ведущей строки – первая, ведущий элемент 5/2. Пересчитав все элементы, получим следующую таблицу:
| xd | cd | B | -3 | |||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x1 | 2/5 | 1/10 | 4/5 | |||||
| x3 | -3 | 1/5 | 3/10 | 2/5 | ||||
| x6 | -1/2 | |||||||
| -11 | -1/5 | -4/5 | -12/5 |
Так как все оценки Dj £ 0, получено оптимальное решение. Оптимальный план имеет следующий вид:
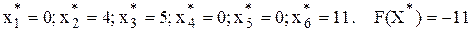
Замечание 1. Если в строке оценок имеются несколько одинаковых максимальных оценок, то в качестве базисной выбирается та переменная xj, для которой коэффициент cj в целевой функции максимальный.
Замечание 2. Если в последней симплекс-таблице нулевые оценки соответствуют только базисным переменным, задача имеет единственное решение. Если же нулевые оценки соответствуют свободным переменным, решение не единственно.
3. Метод искусственного базиса
Как было указано выше, решение ЗЛП симплексным методом начинается с указания какого-либо первоначального опорного плана. Для ЗЛП, записанной в канонической форме, можно непосредственно указать опорный план, если среди векторов Aj, компонентами которых служат коэффициенты при переменных в системе ограничений данной задачи, есть m единичных (т.е., имеются m базисных переменных). Однако, для многих ЗЛП, записанных в канонической форме, не всегда можно сразу определить опорный план. Рассмотрим задачу
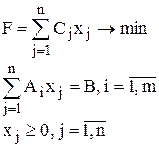
Пусть в данной задаче среди векторов
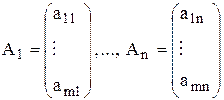 нет единичных.
нет единичных.
В данном случае к каждому i-му уравнению системы ограничений добавляется неотрицательная переменная xn+i , называемая искусственной переменной. Так как введение искусственных переменных, в отличие от дополнительных, меняет множество решений задачи, то они вводятся также и в выражение для целевой функции с очень большим коэффициентом M > 0 (тогда в процессе решения задачи минимизации искусственные переменные будут стремиться к нулю). В результате получается задача, называемая расширенной по отношению к исходной:
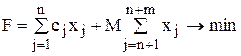
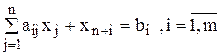
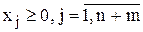
В результате может быть указан первоначальный опорный план. Искусственные переменные при этом приравниваются правым частям (xn+i=bi), остальные – нулю ( 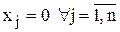 ). Тогда целевая функция примет вид:
). Тогда целевая функция примет вид:
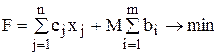 ,
,
а оценки Dj в данном случае будут складываться из двух частей, одна из которых зависит от М, а другая не зависит:
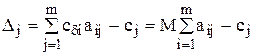
Исходные данные расширенной задачи заносят в симплекс-таблицу, которая содержит на одну строку больше, чем обычная. В последнюю, (m + 2)-ю строку оценок таблицы записывают коэффициенты при M, а в (m + 1)-ю - слагаемые, не содержащие M.
Так как знак Dj определяется знаком коэффициента, стоящего при M, ведущий столбец (и соответственно базисную переменную) выбирают по наибольшему положительному элементу (m + 2)-й строки таблицы. Пересчет симплекс-таблицы при переходе от одного опорного плана к другому производят по общим правилам симплексного метода. Итерационный процесс по (m + 2)-й строке ведут до тех пор, пока
1) либо все искусственные переменные не будут исключены из базиса;
2) либо не все искусственные переменные будут исключены, но (m + 2)-я
строка не содержит больше положительных элементов.
В первом случае полученное базисное решение соответствует некоторому опорному плану исходной задачи, (m+2)-я строка таблицы вычеркивается и решение задачи продолжают обычным симплексными методом. Во втором случае, если элемент, стоящий в (m + 2)-й строке столбца B положителен, задача не имеет решения, если он равен нулю, то базис содержит по крайней мере один из векторов искусственного базиса.
Если в процессе решения задачи какая-либо искусственная переменная выводится их базиса, то соответствующий столбец симплекс-таблицы можно вычеркнуть и не пересчитывать (т.к. эту переменную не имеет смысла вводить ни в один из последующих базисов).
Пример. Решить ЗЛП
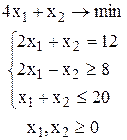
Приведем задачу к канонической форме:
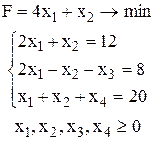
Составим расширенную задачу, вводя искусственную переменную x5 в первое ограничение, а переменную x6 во второе ограничение. Эти же переменные вводятся в целевую функцию с большим коэффициентом M. Расширенная задача имеет вид:
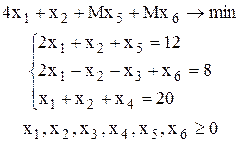
Составим симплекс-таблицу.
| xd | cd | b | M | M | ||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x5 | M | |||||||
| x6 | M | 2 | -1 | -1 | ||||
| x4 | ||||||||
| -4 | -1 | |||||||
Оценки вычисляются следующим образом:
D1 = M × 2 + M × 2 + 0 × 1 – 4 = 4M – 4
D2 = M × 1 + M × (-1) + 0 × 1 – 1 = -1
D3 = M × 0 + M × (-1) + 0 × 0 – 0 = - M + 0
D4 = 0
D5 = 0
D6 = 0
В нижнюю строку оценок записываем коэффициенты при M, в четвертую строку – слагаемые, не содержащие M. Выбор ведущего столбца осуществляется по нижней строке таблицы. В данном случае, в нижней строке имеется единственная положительная оценка. Следовательно, первый столбец выбираем в качестве ведущего. Ведущая строка – вторая. Переменная x1 войдет в базис вместо переменной x6. Переменную x6 не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем шестой столбец не заполняется.
Симплексная таблица после пересчета элементов примет вид:
| xd | cd | b | M | ||||
| x1 | x2 | x3 | x4 | x5 | |||
| x5 | M | 2 | |||||
| x1 | -1/2 | -1/2 | |||||
| x4 | 3/2 | 1/2 | |||||
| -3 | -2 | ||||||
На следующей итерации ведущим столбцом будет второй, ведущей строкой – первая. Переменная искусственная x5 выводится из базиса.
Пересчитываем элементы таблицы:
| xd | cd | B | ||||
| x1 | x2 | x3 | x4 | |||
| x2 | 1 | 1/2 | ||||
| x1 | -1/4 | |||||
| x4 | -1/4 | |||||
| -1/2 |
Так как в строке оценок нет положительных элементов, получен оптимальный план:
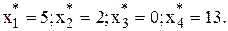
2.4.Двойственность в линейном программировании
Каждой ЗЛП можно поставить в соответствие двойственную в соответствии с следующими правилами:
1) если целевая функция F исходной задачи стремится к минимуму, то целевая функция Ф двойственной задачи – к максимуму и наоборот;
2) число переменных двойственной задачи равно числу ограничений исходной, число ограничений двойственной задачи равно числу переменных исходной. Каждому i-му ограничению исходной задачи соответствует переменная yi двойственной задачи (двойственная переменная), а каждой j-й переменной исходной задачи соответствует j-е ограничение исходной задачи;
3) коэффициентами при переменных целевой функции двойственной задачи являются правые части ограничений исходной задачи, а правыми частями ограничений двойственной задачи являются коэффициенты при целевой функии в исходной задаче;

4) матрица коэффициентов при двойственных переменных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи;
5) для удобства построения двойственных задач рекомендуется в исходной задаче ограничения-неравенства записывать со знаком “£ ” при максимизации и со знаком “ ³” при минимизации;
6) каждому i-му ограничению – неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности (yi³0), а ограничению -равенству - переменная yi произвольного знака;
7) неотрицательной переменной исходной задачи xj³0 соответствует в двойственной задаче j-е ограничение – неравенство, а произвольной переменной xj - равенство. При этом если двойственная задача подлежит минимизации, неравенство записывается со знаком “ ³”, а если двойственная задача подлежит максимизации – со знаком “£ ”.
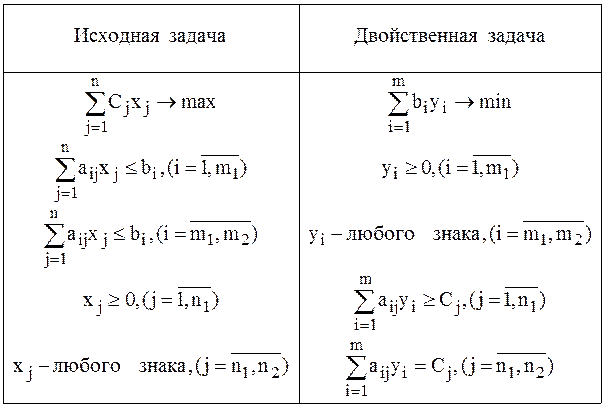 |
Рассмотренные правила построения двойственных задач иллюстрируются табл. 8.
Таблица 8
Соотношение двойственности является взаимным, то есть задача двойственная по отношению к двойственной совпадает с исходной.
Пример Построить двойственную задачу к задаче определения производственного плана, приведенной в примере 1: определить, сколько продукции каждого вида xj необходимо изготовить, чтобы при заданной прибыли от реализации единицы продукции cj и заданных размерах имеющихся ресурсов bi максимизировать общую прибыль.
Математическая модель задачи из примера 1 формулировалась следую-щим образом:
F=7x1+3x2+6x3+12x4®max;
3x1+x2+2x3+4x4 £440;
x1+8x2+6x3+2x4 £200;
x1+4x2+7x3+2x4 £320;
xj ³0, j= 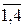 .
.
Введя три двойственные переменные y1 , y2 , y3 , в соответствии с приве-денными выше правилами построим двойственную задачу:
Ф=440у1+200y2+320у3®min;
3y1+y2+y3 ³7;
y1+8y2+4y3 ³3;
2y1+6y2+7y3³6;
4y1+2y2+2y3 ³12;
yi ³0, j= 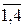 .
.
Отсюда видно, что двойственная задача заключается в определении стоимости единицы ресурса yi, чтобы при заданных количествах ресурсов bi и заданной прибыли cj от реализации единицы продукции минимизировать общую стоимость ресурсов.
Пара взаимодвойственных задач, в которых все ограничения записываются в виде неравенств, причем при максимизации знаки всех неравенств £, а при минимизации ³, называется симметричной. Приведенная выше пара задач симметрична.
Дата добавления: 2021-07-22; просмотров: 547;











