Критерий Байеса-Лапласа

Для построения оценочной функции при данном критерии используется априорная информация о вероятностных 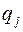появления внешних условий.

Множество оптимальных вариантов решения определяется соотношением

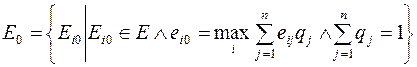(8.2)

Правило выбора решения в соответствии с критерием Байеса-Лапласа интерпретируется следующим образом.

Матрица решений 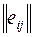дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк. Выбираются те варианты 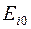, в строках которых стоят наибольшие значения 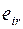этого столбца.

При этом ситуация, в которой принимаются решение, характеризуется следующими обстоятельствами

– вероятности появления состояний 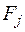известны;

– решение реализуется (теоретически) бесконечно много раз;

– для малого числа реализаций решения допускается некоторый риск.

При достаточно большом количестве реализаций риск практически полностью исключен.

Позиция ЛПР на основе критерия Байеса-Лапласа, более оптимистична, чем по минимаксному критерию, однако она предполагает более высокий уровень информированности.

Критерий Сэвиджа

Этот критерий основывается на предварительном преобразовании матрицы системных оценок в матрицу остатков.

Множество оптимальных вариантов решения определяется соотношением

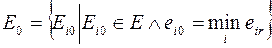(8.3)

Соответствующее критерию Сэвиджа правило выбора интерпретируется следующим образом.

Каждый элемент матрицы решений 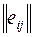вычитается из наибольшего результата 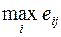соответствующего столбца. Разности 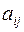образуют матрицу остатков 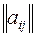. Эта матрица пополняется столбцом наибольших разностей 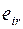. Выбираются те варианты 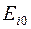, в строках которых стоит наименьшее для этого столбца значение.

Величины 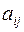можно интерпретировать как потери (штрафы), возникающие в состоянии 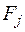при замене оптимального для него варианта .

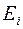Критерий Гурвица

Правило выбора согласно критерию Гурвица формулируется следующим образом.

Матрица решений 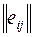дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки. Выбираются те варианты 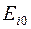, в строках которых стоят наибольшие элементы 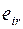этого столбца.

Множество оптимальных вариантов решения определяется соотношением

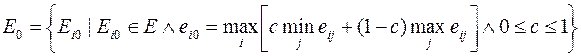(8.4)

с – весовой множитель, для с=1 критерий Гурвица превращается в минимаксный, для с=0 он превращается в критерий азартного игрока. В технических приложениях бывает достаточно трудно выбрать критерий, поэтому чаще всего весовой множитель с=0,5 без возражений принимается в качестве некоторой «средней» точки зрения. При обосновании выбора применяют обратный порядок действий. Для приглянувшегося решения вычисляют весовой множитель с, и он интерпретируется как показатель соотношения оптимизма и пессимизма.

Данный критерий предъявляет к ситуации, в которой принимается решение, следующие требования:

- о вероятностях появления состояний 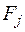ничего не известно;

- с появление состояний 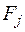необходимо считаться;

- реализуется лишь малое количество решений;

- допускается некоторый риск.