Задача коммивояжера
Имеются n пунктов или городов с заданными расстояниями 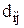 между i-м и j-м пунктами. Необходимо составить оптимальный маршрут из условия минимизации суммарного расстояния для коммивояжера, выходящего из пункта с номером 1, который должен побывать во всех пунктах ровно по одному разу и вернуться в исходный пункт.
между i-м и j-м пунктами. Необходимо составить оптимальный маршрут из условия минимизации суммарного расстояния для коммивояжера, выходящего из пункта с номером 1, который должен побывать во всех пунктах ровно по одному разу и вернуться в исходный пункт.
Введем альтернативные бинарные переменные :
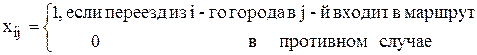 .
.
Условия минимизации общего расстояния , а также прибытия в каждый пункт и выезда из него ровно по одному разу могут быть выражены следующим образом:

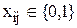 .
.
Однако необходимо обеспечить непрерывность маршрута, чтобы набор звеньев, входящих в маршрут, образовывал единую цепочку (например, при n=8 цепочка (1,2) - (2,6) - (6,4) - (4,8) - (8,5) - (5,3) - (3,7) - (7,1)), а не состоял бы из отдельных не связанных цепочек (например, (1,2) - (2,6) - (6,1) и (3,8) - (8,7) - (7,5) - (5,4) - (4,3)). Для устранения замкнутых циклов (подобходов), включающих количество вершин меньшее n, в модель вводятся n дополнительные переменных ui³0 ( 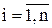 ) и n2 дополнительных ограничений:
) и n2 дополнительных ограничений:
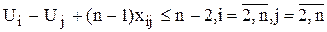 .
.
Действительно, пусть маршрут включает несколько цепочек. Тогда существует цепочка, начинающаяся и заканчивающаяся в начальном пункте, но включающая n1 звеньев, где n1<n. Просуммировав эти неравенства вдоль такой цепочки (т.е. при xik=1), получим бессмысленное неравенство n1(n-1)£n1(n-2) (все ui и uj при суммировании взаимно уничтожаются). Покажем теперь, что для маршрута, исключающего подобходы, это неравенство выполняется, т.е., можно найти значения ui, удовлетворяющие дополнительным ограничениям. Положим ui=p, если город i посещается коммивояжером на p-м шаге, p= 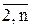 . Отсюда следует, что
. Отсюда следует, что 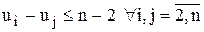 . Таким образом, ограничения выполняются для всех
. Таким образом, ограничения выполняются для всех 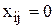 . При
. При 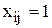 эти ограничения превращаются в равенства
эти ограничения превращаются в равенства
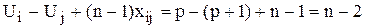 .
.
Задача коммивояжера имеет широкий круг практических приложений. К ней сводятся задачи оптимальной маршрутизации (выбор маршрутов перевозки грузов, маршрутов движения транспорта, минимизация расстояния, проходимого исполнительным механизмом станка с ЧПУ и т.д.), задачи проектирования электрических и вычислительных сетей, задачи определения последовательности обработки деталей на станках с условием минимизации времени переналадок и т.д.
Пример 11. Пусть необходимо проложить коммуникации между n различными ЭВМ таким образом, чтобы каждая ЭВМ была связана с двумя соседними, вся сеть была бы подключена к центральной ЭВМ, а суммарная длина коммуникаций была бы минимальна. . Заданы расстояния dij между i-й и j-й ЭВМ.
Данная задача формализуется в виде задачи коммивояжера следующим образом:
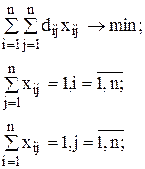
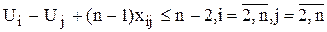 ;
;
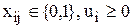 .
.
При этом xij=1, если i-я и j-я ЭВМ соединяются.
Задача о покрытии
Пусть имеется n предметов, каждый из которых обладает некоторым числом признаков из заданного множества m признаков, а в совокупности эти n предметов обладают всеми m признаками. Необходимо выбрать минимальное число предметов, которые в совокупности обладали бы m признаками. Условия задачи задаются матрицей A с элементами
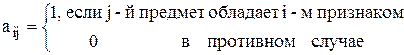
Введем бинарные переменные:
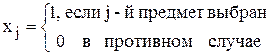 .
.
Тогда математическая модель задачи имеет следующий вид:
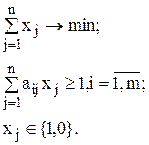
Каждое i-е ограничение в данном случае показывает, что должен быть выбран хотя бы один предмет, обладающий i-м признаком.
Если каждому j-му предмету приписывается вес 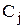 , может быть сформулирована взвешенная задача о покрытии:
, может быть сформулирована взвешенная задача о покрытии:
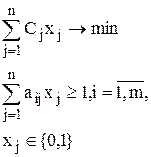
Если каждому i-му признаку приписывается натуральное число 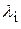 и требуется найти минимальное число таких предметов, что i-м признаком обладает не менее
и требуется найти минимальное число таких предметов, что i-м признаком обладает не менее 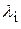 предметов из указанного набора, получаем задачу о кратном покрытии:
предметов из указанного набора, получаем задачу о кратном покрытии:
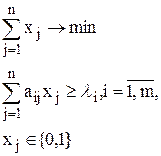
Задача о разбиении. Задача о разбиении аналогична задачи о покрытии с тем отличием, что признаки у различных предметов не должны совпадать:
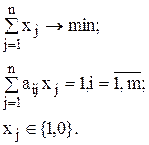
Задача о взвешенном разбиении формулируется следующим образом:
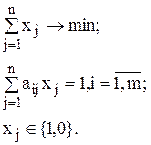
К задаче о покрытии сводится широкий круг задач информационного поиска, синтеза логических схем, задачи разбиения электронных схем на модули и покрытия схем типовыми ячейками и т.д.
Пример 12. Пусть некоторое количество информации хранится в n массивах (файлах) длины 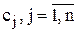 , причем на каждую единицу информации отводится по крайней мере один массив. Задана матрица T с элементами
, причем на каждую единицу информации отводится по крайней мере один массив. Задана матрица T с элементами
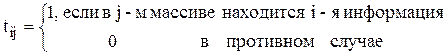
Получена заявка на m типов единиц информации. Необходимо определить подмножество массивов минимальной длины, необходимых для удовлетворения заявки.
Введем бинарные переменные:
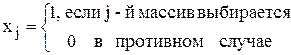 .
.
Тогда математическая модель задачи формализуется в виде задачи о покрытии:
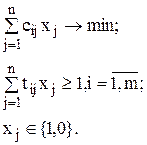
Методы решения задач целочисленного программирования
Методы решения задач целочисленного программирования делятся на следующие группы:
методы отсечения;
комбинаторные методы;
приближенные методы.
Методы отсечения используются только для решения линейных задач, а комбинаторные и приближенные методы - как для линейных, так и для нелинейных задач.
Метод отсечения Гомори решения задач целочисленного линейного программирования
Рассмотрим задачу целочисленного линейного программирования:
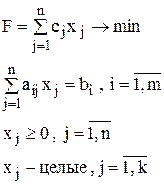
При k = n задача является полностью целочисленной, при k < n – частично целочисленной.
Решение таких задач сводится к решению конечной последовательности специально построенных ЗЛП: P0 , P1 ,…, Pl ,…, Pn , каждая из которых получается из предыдущей путем добавления к ее условиям дополнительного линейного ограничения (неравенства), называемого правильным отсечением (или сечением). При этом l-м сечением называется линейное ограничение, вводимое в задачу Pl-1 , для образования задачи Pl и удовлетворяющее двум условиям:
1) любое целочисленное решение задачи Pl-1 ему удовлетворяет;
2) любое нецелочисленное решение задачи Pl-1 ему не удовлетворяет
(отсекается).
Пусть задача Pl-1 решена симплексным методом и ее решение не удовлетворяет условиям целочисленности. Введем обозначения: [a]- целая часть числа a, т.е., наибольшее целое число, не превосходящее a;
{a} = a – [a] - дробная часть числа a.
B - Множество индексов базисных переменных из последней симплекс-таблицы;
S - Номер строки из последней симплексной таблицы с наибольшим значением {bi}, 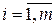 .
.
Тогда сечение Гомори для решения полностью целочисленной задачи запишется в виде:
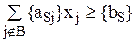
Решение целочисленных задач включает следующую последовательность этапов:
1. Определение оптимального решения ЗЛП без учета условий целочисленности.
2. Если полученное решение является целочисленным, то алгоритм заканчивает работу (оптимальное решение найдено), в противном случае осуществляется переход к шагу 3.
3. На основании последней симплекс-таблицы, полученной при решении ЗЛП, записывается сечение Гомори .
4. Добавление ограничения построенного на предыдущем этапе к условиям решаемой задачи. Для этого данное ограничение преобразуется в уравнение
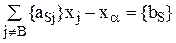
где 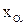 – дополнительная неотрицательная переменная.
– дополнительная неотрицательная переменная.
Затем полученное уравнение умножается на –1
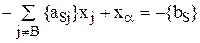 (для I сечения)
(для I сечения)
и добавляется к последней симплекс-таблице. Далее полученная задача решается двойственным симплекс-методом.
5. Переход к шагу 1.
Двойственный симплекс-метод
Двойственный симплекс-метод используется при нахождении решения задачи ЛП, записанной в канонической форме, для которой среди векторов Аj , составленных из коэффициентов при неизвестных в системе ограничений, имеются m- единичных. Вместе с тем ДСМ можно применять при решении ЗЛП, правые части ограничения которой могут быть отрицательным числом.
 |
Рассмотрим ЗЛП, записанную в канонической форме.
 Допустим, что выбран такой базис (A1,...,AL ,...,Am), при котором хотя бы из правых частей ограничений отрицательна, но для всех
Допустим, что выбран такой базис (A1,...,AL ,...,Am), при котором хотя бы из правых частей ограничений отрицательна, но для всех
Тогда решение X=(b1,…,bL,…,bm,0,…,0) системы линейных алгебраических уравнений, задающей ограничения, называется псевдопланом ЗЛП. Псевдоплан не является планом исходной ЗЛП, так как некоторые его компоненты отрицательны.
 Очевидно, что для получения оптимального плана исходной ЗЛП необходимо из столбца в (правых частей ограничений) симплекс-таблицы все отрицательные элементы. При этом должно выполнятся условие:
Очевидно, что для получения оптимального плана исходной ЗЛП необходимо из столбца в (правых частей ограничений) симплекс-таблицы все отрицательные элементы. При этом должно выполнятся условие:
Основные шаги алгоритма:
1. Нахождение псевдоплана задачи.
2. Составление симлекс- таблицы.
3. Проверка псевдоплана на оптимальность. Если псевдоплан оптимален
(все правые части 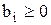 , а все оценки
, а все оценки 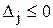 ) решение задачи найдено. В противном случае необходимо перейти к следующему шагу.
) решение задачи найдено. В противном случае необходимо перейти к следующему шагу.
4.
 |
Выбор ведущей строки. При этом в столбце правых частей ограничений выбирается наименьший отрицательный элемент и строка, которой он соответствует, объявляется ведущей строкой.
 |
или
Если в ведущей строке l все элементы неотрицательны, то целевая функция двойственной задачи не ограничена на множестве допустимых значений (задача не имеет решения).
Если в l-й строке существуют элементы alj < 0, то осуществляется выбор ведущего столбца.
5. Выбор ведущего столбца. При этом для l-й ведущей строки
определяются отношения 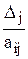 для alj < 0, среди них выбираются
для alj < 0, среди них выбираются
 |
минимальные. Столбец, которому соответствует минимальное отношение, объявляется ведущим столбцом:
6 Пересчет элементов симплекс-таблицы по правилу
прямоугольника. Переход к шагу 3.
Пример. Решить задачу целочисленного линейного программирования методом Гомори:
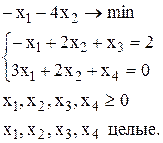
Решаем данную задачу симплекс-методом без учета условий целочисленности.
| xd | cd | b | -1 | -4 | ||
| x1 | x2 | x3 | x4 | |||
| x3 | -1 | 2 | ||||
| x4 | ||||||
| x2 | -4 | -1/2 | 1/2 | |||
| x4 | 4 | -1 | ||||
| -4 | -2 | |||||
| x2 | -4 | 3/2 | 3/8 | 1/8 | ||
| x1 | -1 | -1/4 | 1/4 | |||
| -7 | -5/4 | -3/4 |
Полученное решение не является целочисленным. Поэтому переходим к построению дополнительного ограничения. Для этого необходимо выбрать ту строку таблицы, которой соответствует максимальная дробная часть элементов столбца свободных членов b. В данном случае единственная строка с нечелочисленным значение bi – первая (S = 1). Записываем первое сечение Гомори:
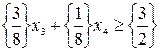 или
или 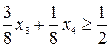
Умножив левую и правую часть на 2, получим:
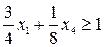
Добавим к левой части дополнительную переменную x5 и умножим полученное равенство на –1. В результате получим:
(*) 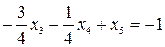
Добавим полученное ограничение к последней симплекс-таблице и решим полученную задачу с использованием двойственного симплекс-метода:
| Xd | cd | b | -1 | -4 | |||
| x1 | x2 | x3 | x4 | x5 | |||
| X2 | -4 | 3/2 | 3/8 | 1/8 | |||
| X1 | -1 | -1/4 | 1/4 | ||||
| x5 | -1 | -3/4 | -1/4 | ||||
| -7 | -5/4 | -3/4 | |||||
| x2 | -4 | 1/2 | |||||
| x1 | -1 | 4/3 | 1/3 | -1/3 | |||
| x3 | 4/3 | 1/3 | -4/3 | ||||
| -16/3 | -1/3 | -5/3 |
Полученное оптимальное решение не является целочисленным, по этому опять переходим к построению сечения Гомори. Так как значения дробных частей свободных членов b2 и b3 одинаковы, строку для построения дополнительного ограничения выбираем произвольно (например, S = 2). Тогда ограничение записывается в виде:
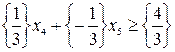 или
или 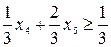
После соответствующих преобразований получим:
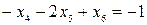
Добавим данное ограничение к последней симплекс-таблице и решим полученную задачу двойственным симплекс-методом:
| xd | cd | b | -1 | -4 | ||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x2 | -4 | 1/2 | ||||||
| x1 | -1 | 4/3 | 1/3 | -1/3 | ||||
| x3 | 4/3 | 1/3 | -4/3 | |||||
| x6 | -1 | -1 | -2 | |||||
| -16/3 | -1/3 | -5/3 | ||||||
| x2 | -4 | -1/2 | ||||||
| x1 | -1 | -1 | 1/3 | |||||
| x3 | -6 | 1/3 | ||||||
| x4 | -1 | |||||||
| -5 | -1 | -1/3 |
Полученное целочисленное решение является оптимальным решением исходной задачи: 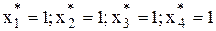 .
.
Метод ветвей и границ
Метод ветвей и границ основан на использовании конечности множества допустимых вариантов и замене полного перебора сокращенным направленным перебором. При этом полного перебора удается избежать за счет отбрасывания неперспективных множеств вариантов, т.е. тех множеств, где заведомо нет оптимального решения. В методе ветвей и границ все множество допустимых вариантов последовательно дробится на все меньшие подмножества. При этом вычисляются оценки (границы), которые позволяют сделать вывод о том, какое из полученных подмножеств может быть отброшено при условии сохранения подмножества, содержащего оптимальное решение. Для иллюстрации работы МГ используется дерево, называемое деревом перебора (вариантов).
Рассмотрим частично целочисленную задачу следующего вида:
Максимизировать Z = СX
при ограничениях AX = B, 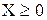 ,
,
хj - целочисленная переменная при jÎI,
где I - множество индексов целочисленных переменных задачи. Задача записана в векторной форме: С=(с1…сn) - вектор-строка коэффициентов целевой функции; X= 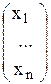 - вектор столбец переменных задачи; В=
- вектор столбец переменных задачи; В=  - вектор-столбец правых частей; A=
- вектор-столбец правых частей; A= 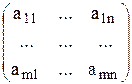 - матрица коэффициентов при переменных в системе ограничений.
- матрица коэффициентов при переменных в системе ограничений.
В качестве первого шага необходимо решить сформулированную задачу ЛП, рассматривая все ее переменные как непрерывные. Получаемая таким образом задача ЛП обозначается через ЛП-1, оптимальное значение ее целевой функции - через Z1. Пусть в оптимальном решении задачи ЛП-1 некоторые целочисленные переменные принимают дробные значения; тогда оптимальное решение исходной задачи не совпадает с оптимальным решением ЛП-1. В этом случае величина Z1 представляет собой верхнюю границу оптимального значения Z исходной задачи.
На следующем шаге проводится ветвление по одной из целочисленных переменных, имеющих дробное значение в оптимальном решении задачи ЛП-1. Для определения переменной, по которой производится ветвление, разработан ряд правил. Приведем некоторые из них.
1. Выбор целочисленной переменной с наибольшей дробной частью.
2. Приписывание целочисленным переменным приоритетов и ветвление по переменной с наибольшим приоритетом. Важность целочисленной переменной может определяться следующими соображениями:
- данная переменная является наиболее важной, ее значение ирает важную роль в модели по мнению разработчиков.
- коэффициент целевой функции при данной переменной превосходит остальные;
3. Находится то дополнительное ограничение, которое приводит к наибольшему возрастанию нижней границы. Цель - найти ту вершину, которая наиболее верно будет отброшена.
4. Произвольные правила выбора. Например, можно выбирать переменную с наименьшим номером.
Пусть ветвление происходит по целочисленной переменной хj, дробное значение которой в оптимальном решении ЛП-1, равно bj . Далее рассматриваются две новые задачи ЛП, обозначаемые через ЛП-2 и ЛП-3. Они получаются путем введения ограничений 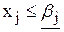 и
и 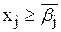 соответственно, где через
соответственно, где через 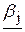 обозначается наибольшее целое, не превосходящее bj , через
обозначается наибольшее целое, не превосходящее bj , через 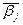 - наименьшее целое, большее
- наименьшее целое, большее 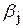 . Условия задачи ЛП-2 и ЛП-3 можно записать следующим образом:
. Условия задачи ЛП-2 и ЛП-3 можно записать следующим образом:
ЛП-2 ЛП-3
Максимизировать Z=СX Максимизировать Z=CX
при ограничениях AX=B, при ограничениях AX=B,
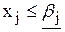
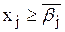
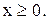
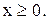
Допустим, что оптимальные решения задач ЛП-2 и ЛП-3 также содержат дробные значения целочисленных переменных и поэтому не являются допустимыми для исходной задачи.
На следующем шаге необходимо выбрать задачу ЛП-2 или ЛП-3 и произвести ветвление в соответствующей вершине, вводя новое ограничение. Выбор вершины (задачи ЛП) для дальнейшего ветвления осуществляется с помощью специальных правил. Приведем некоторые из них.
1. Использование оптимального значения целевой функции. Для дальнейшего ветвления следует выбирать вершину, соответствующую наибольшему оптимальному значению целевой функции задачи ЛП. Некоторым обоснованием этого правила служит то соображение, что допустимая область задачи ЛП с наибольшим значением Z может содержать и хорошее целочисленное решение. Например, любое целочисленное решение, полученное ветвлением задачи ЛП-2, не может давать значение Z, лучше, чем оптимальное значение Z в задаче ЛП-2.
2. Правило "последним пришел - первым обслужен". Для дальнейшего ветвления выбирается (произвольным образом) задача ЛП, решавшаяся последней.
После выбора вершины для дальнейшего ветвления выбирается целочисленная переменная, которая имеет в оптимальном решении соответствующей задачи ЛП дробное значение, и производится ветвление по этой переменной. Процесс ветвления и решения задачи продолжается до получения целочисленного оптимального решения одной из задач ЛП. Значение Z в полученной точке представляет собой нижнюю границу оптимального значения целевой функции исходной задачи ЦЛП. На этом этапе определяются прозондированные вершины, т.е. вершины, в которых дальнейшее ветвление невозможно или нецелесообразно. Вершина является прозондированной, если она удовлетворяет одному из следующих условий:
1.Оптимальное решение, соответствующее данной вершине, целочисленно. В этом случае полученное решение допустимо для исходной задачи ЦЛП.
2. Задача ЛП, соответствующая рассматриваемой вершине, не имеет допустимых решений.
3. Оптимальное значение Z соответствующей задачи ЛП не превосходит текущей нижней границы.
Во втором и третьем случаях прозондированные вершины отбрасываются. Процесс решения задачи продолжается до тех пор, пока все вершины не будут прозондированы. Прозондированная вершина, соответствующая целочисленному решению с наилучшим (наибольшим) значением целевой функции дает оптимальное решение исходной задачи.
Пример 14. Для иллюстрации основных принципов метода ветвей и границ рассмотрим следующую задачу целочисленного программирования.
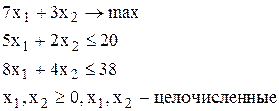
Начальный шаг решения этой задачи состоит в нахождении решения задачи линейного программирования, получаемой при отбрасывании условия целочисленности x1 и x2. Обозначим эту задачу через ЛП-1. Ее оптимальное решение имеет вид x1=1, x2=7.5, оптимальное значение целевой функции Z1=29.5. Поскольку x2 принимает дробное значение, найденное решение не может быть оптимальным решением исходной целочисленной задачи. Найденное значение Z1 представляет собой верхнюю границу истинного оптимального целочисленного значения, поскольку при выполнении требования целочисленности x2 значение Z может лишь уменьшиться.
Следующий шаг метода ветвей и границ состоит в разбиении задачи ЛП-1 на две подзадачи , первая из которых (ЛП-2) образуется в результате добавления к задаче ЛП-1 ограничения 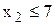 , а вторая (ЛП-3) - в результате добавления ограничения
, а вторая (ЛП-3) - в результате добавления ограничения 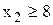 :
:
ЛП-2 ЛП-3
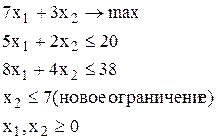
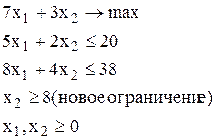
Дерево возможных вариантов представлено на рис. 33. Оптимальное решение задачи ЛП-3 - точка х1=0.75, х2=8, где Z2=29,25. Оптимальное решение задачи ЛП-2 точка х1=1.2, х2=7, где Z3=29,4. Для дальнейшего ветвления выберем задачу ЛП-2, т.к. значение целевой функции в ней больше. К задаче ЛП-2 добавим ограничения 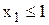 , (задача ЛП-4) и
, (задача ЛП-4) и 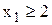 (задача ЛП-5). Результаты решения задачи ЛП-4: х1=1, х2=7, где Z4=28. Результаты решения задачи ЛП-5: х1=2, х2=5, где Z5=29.
(задача ЛП-5). Результаты решения задачи ЛП-4: х1=1, х2=7, где Z4=28. Результаты решения задачи ЛП-5: х1=2, х2=5, где Z5=29.
Таким образом, получены два допустимых (целочисленных) решения исходной задачи целочисленного программирования, причем значение Z4=29 представляет собой нижнюю границу максимального значения Z для задачи целочисленного программирования. Даже если исходная задача имеет другие целочисленные решения, значение целевой функции в них не может быть больше 29. Таким образом, значение Z4=29 представляет собой нижнюю границу максимального значения Z для исходной целочисленной задачи. Вершины ЛП-4 и ЛП-5 являются прозондированными (так как в них получено целочисленное решение, а в процессе дальнейшего ветвления оно может лишь ухудшаться). Ветвление вершины ЛП-3 также нецелесообразно в связи с тем, что целевая функция исходной задачи может принимать только целочисленные значения (т.к. все переменные и коэффициенты целочисленны), а при дальнейшем ветвлении ее значения будут увеличиваться (т.е., станут больше 29). Следовательно, оптимальное решение задачи х1=2, х2=5, где Z5=29.
Метод ветвей и границ может применяться для решения не только линейных, но и нелинейных целочисленных задач. Он также может использоваться для решения задач с дискретными переменными.

|
Принятие решений
Под принятием решения (ПР) понимается выбор одного 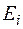 или нескольких вариантов решения задачи из некоторого исходного множества вариантов (альтернатив)
или нескольких вариантов решения задачи из некоторого исходного множества вариантов (альтернатив) 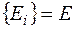 .
.
В формализованном виде вариантом (альтернативой) 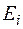 называется один из способов построения системы, выбора стратегии и т.д., допускающий определение результата
называется один из способов построения системы, выбора стратегии и т.д., допускающий определение результата 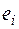 . Другими словами, с вариантом
. Другими словами, с вариантом 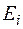 связана оценка
связана оценка 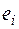 , ему соответствующая.
, ему соответствующая.
В дальнейшем будем полагать, что имеется конечное число вариантов (альтернатив) 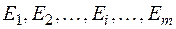 .
.
Принятие решений происходит из многих вариантов 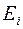 , соответствующих различным условиям (состояниям)
, соответствующих различным условиям (состояниям) 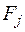 , поэтому совокупность оценок образует матрицу системных оценок
, поэтому совокупность оценок образует матрицу системных оценок 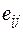 (таблица 1). Термин «системные оценки» отражает факт рассмотрения всей совокупности условий, в которых осуществляется процесс принятия решений.
(таблица 1). Термин «системные оценки» отражает факт рассмотрения всей совокупности условий, в которых осуществляется процесс принятия решений.
Решение – подмножество множества вариантов (альтернатив), образованное на основе системы предпочтений.
Под решением (см. таблицу 1.) будем понимать оценку, соответствующую варианту 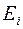 и условиям
и условиям 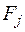 , причем оценка
, причем оценка 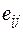 может характеризовать экономический эффект (прибыль), полезность, рациональность или надежность решения.
может характеризовать экономический эффект (прибыль), полезность, рациональность или надежность решения.
Метод системных матриц широко распространен в задачах принятия решений, поскольку в естественной форме представляет наборы вариантов и условий построения схем функционирования сложных систем.
Матрицей системных оценок (матрицей решений) называется матрица следующего вида (таблица 1).
Принятие решений должно обеспечить выбор пары 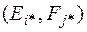 , которая является предпочтительной с точки зрения некоторого критерия оптимальности, рациональности, полезности.
, которая является предпочтительной с точки зрения некоторого критерия оптимальности, рациональности, полезности.
Таблица 1 – Матрица системных оценок (матрица решений)
| ВАРИАНТЫ | УСЛОВИЯ | |||||
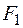
| 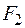
| 
| 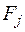
| 
| 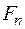
| |
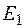
| 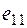
| 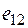
| 
| 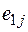
| 
| 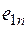
|
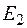
| 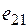
| 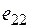
| 
| 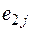
| 
| 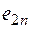
|

| 
| 
| 
| 
| 
| 
|
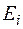
| 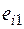
| 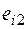
| 
| 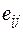
| 
| 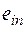
|

| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 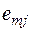
| 
| 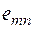
|
Дата добавления: 2021-07-22; просмотров: 867;











