Аналитическое решение заданного уравнения

Уравнение

у' – у = -2ху^-1

есть уравнение Бернулли. Проинтегрируем его методом Бернулли, для чего положим у = uv, где u и v две неизвестные функции. Тогда исходное уравнение преобразуется к следующему:

u'v – v'u – uv = -2x(uv)^-1

или

u(v'–v)+ u'v = -2x(uv)^-1 . (*)

Функцию v выберем из условия v' – v = 0, причем возьмем частное решение этого дифференциального уравнения v = е^х.

Подставив v в уравнение (*), получаем u' е^х= -2хu^-1е^-х,

а это – уравнение с разделяющими переменными. Решая его, находим

u² = с +2хе^-2х+ е^-^2х .

Так как решение исходного уравнения есть произведения функций u и v, то получаем .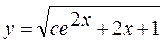

При начальном условии у(0) = 1 получим

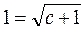Таким образом, искомое частное решение имеет вид

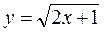Сравнение точного решения и приближенных решений исходного дифференциального уравнения

Таблица 6

	0,2	0,4	0,6	0,8	1,0	в точке х = 1,0
Абсолют. погрешн.	Относит. погрешн.
точное	1,1832	1,3416	1,4832	1,6124	1,7320
по методу Эйлера	1,2000	1,3733	1,5294	1,6786	1,8237	0,0917	5,3%
по модиф. методу Эйлера	1,1836	1,3426	1,4850	1,6152	1,7362	0,0042	0,24%
по методу Рунге- Кутта	1,1832	1,3417	1,4833	1,6125	1,7321	0,0001	0,006%

Контрольная работа №7

Пусть дано:

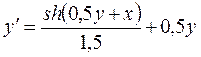;у(0) = 0; x 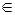[0,0,2]; .

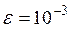Для выбора шага интегрирования вычислим решение в точке х = 0,1 с шагом h = 0,1(табл.7) и с шагом h = 0,05 (табл.8).

Таблица 7

х	у	sh(0,5y+x)	f (x,y)	k =hf (x,y)	Δу

0,05		0,05002	0,0334	0,00334	0,00668
0,05	0,00167	0,5087	0,0347	0,00347	0,00694
0,1	0,00347	0,10192	0,0697	0,00697	0,00697
					0,00343
0,1	0,00343

В таблицах .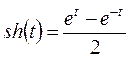

Таблица 8

х	у	sh(0,5y+x)	f(x,y)	k=hf(x,y)	Δу

0,025		0,02500	0,01667	0,000834	0,001668
0,025	0,000417	0,02521	0,01702	0,000851	0,001702
0,05	0,000851	0,0545	0,03406	0,001703	0,001703
	0,000846
0,05	0,000846	0,05044	0,03405	0,001702	0,001702
0,075	0,001697	0,07592	0,05146	0,002573	0,005146
0,075	0,002132	0,07614	0,05183	0,002592	0,005184
0,1	0,003438	0,10190	0,06965	0,003482	0,003482
	0,002586
0,1	0,003432

Так как полученные результаты совпадают в пределах заданной точности, вычисления продолжим с шагом h = 0,1 и с шагом h = 0,2.

Результаты вычислений помещены в табл.9 и табл.10 соответственно.

Таблица 9

х	у	sh(0,5y+x)	f(x,y)	k=hf(x,y)	Δу
0,1	0,003432	0,10190	0,06965	0,006965	0,006965
0,15	0,006914	0,15406	0,10617	0,01617	0,021234
0,15	0,008740	0,15499	0,10770	0,010770	0,021540
0,2	0,014202	0,20858	0,14615	0,014615	0,014615
	0,010726
0,2	0,014158

Таблица 10

х	у	sh(0,5y+x)	f(x,y)	k=hf(x,y)	Δу

0,1		0,10017	0,06678	0,013356	0,026712
0,1	0,006678	0,10352	0,07235	0,014470	0,028940
0,2	0,014470	0,20872	0,14638	0,029276	0,029276
					0,014155
0,2	0,014155

Сравнение результатов расчета, полученных с шагом h = 0,1 и с шагом h = 0,2, показывает, что с точностью до ε = 10^-3можно принять у(0,2) ≈ 0,014158 и что в дальнейшем шаг расчета следовало бы снова удвоить.