Критерий Ходжа-Лемана

Критерий Ходжа-Лемана, опирающийся на минимаксный критерий и критерий Байеса-Лапласа, характеризуется тем, что с помощью параметра 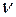выражает степень доверия к используемому распределению вероятностей. При 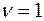критерий переходит в критерий Байеса-Лапласа, а при 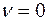– в минимаксный. При этом выбор параметра 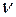подвержен субъективизму.

Правило выбора формулируется следующим образом.

Матрица решений 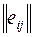дополняется столбцом, составленным из средних взвешенных (с постоянными весами) математического ожидания и наименьшего результата каждой строки. Отбираются те варианты решений 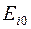, в строках которых стоит наибольшее значение этого столбца.

Множество оптимальных вариантов решения определяется соотношением

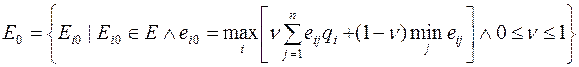(8.5)

Ситуация, в которой рекомендовано применение этого критерия, характеризуется следующими условиями:

– вероятности появления состояний 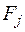неизвестны, но некоторые предположения о распределениях вероятностей возможны;

– принятое решение теоретически допускает бесконечно много реализаций:

– при малых числах реализации допускается некоторый риск.

Критерий Гермейера

Правило выбора согласно этому критерию формулируется следующим образом.

Матрица решений 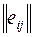дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния 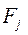. Выбираются те варианты 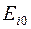, в строках которых находится наибольшее значение 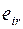этого столбца.

Множество оптимальных вариантов решения определяется соотношением

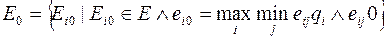(8.6)

Критерий Гермейера применяется в хозяйственных задачах и ориентирован на цены и затраты, то есть на отрицательные значения 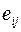матрицы оценок ( 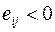). Если среди величин 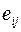встречаются положительные, тогда необходимо перейти к строго отрицательным значениям с помощью преобразования 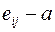, при .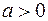

Условия применения критерия Гермейера:

– вероятности появления состояний 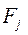известны;

– с появлением тех или иных состояний, отдельно или в комплексе, необходимо считаться;

– допускается некоторый риск;

– решение может реализоваться один или много раз.

Если функция распределения известна не очень надежно, а числа реализаций малы, то, следуя критерию Гермейера, получают неоправданно большой риск.