Законы булевой алгебры

При сочетаниях двух и более переменных для преобразования логических функций используют следующие законы булевой алгебры:

1. Переместительный закон – порядок записи переменных не влияет на результат (переменные можно менять местами). Имеет аналог в обычной алгебре.

+

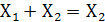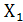
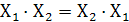
2.Сочетательный закон (ассоциативный). Можно производить объединение переменных в скобки.

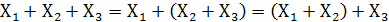
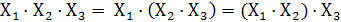
3.Распределительный закон (дистрибутивный)

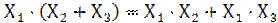
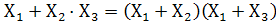не имеет аналога в обычной алгебре, поэтому докажем путем почленного перемножения скобочных выражений правой части:

(Х₁ + Х₂)×(Х₁ + Х₃) = Х₁×Х₁ + Х₁×Х₃ + Х₁×Х₂ + Х₂×Х₃ =Х₁ + Х₁×Х₃ + Х₁×Х₂ + Х₂×Х₃ = Х₁×(1 + Х₃ + Х₂) + Х₂×Х₃ = Х₁ + Х₂×Х₃, что и требовалось доказать.

4.Закон поглощения

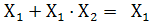
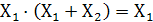
Докажем первое выражение:

=

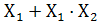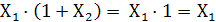
Докажем второе выражение:

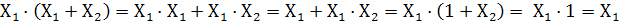
5.Закон склеивания

=

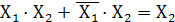
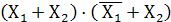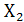
Докажем первое выражение:

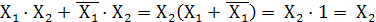
Докажем второе выражение:

=

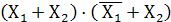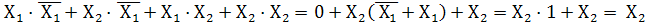
6.Закон инверсии или правило де Моргана. (Огастес де Морган – 1806-1871 шотландский математик и логик, независимо от Джорджа Буля пришел к основным идеям математической логики).

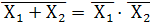; Инверсия дизъюнкции переменных есть конъюнкция инверсий этих же переменных.

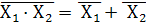Соответственно: Инверсия конъюнкции переменных есть дизъюнкция инверсий этих же переменных

или

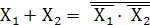; Дизъюнкция переменных есть инверсия конъюнкции инверсий этих же переменных.

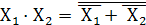
7.Закон повторений или тавтологии:

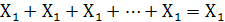
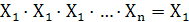
8.Закон двойной инверсии

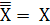; Четное количество инверсий может быть отброшено.

Логические функции Л.Ф.

Л.Ф. называется функция двоичных переменных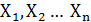

Y = (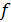

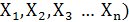
Операции дизъюнкции, конъюнкции и инверсии служат примерами простейших логических функций.

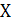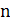Если число аргументов равно , то число возможных комбинаций значений аргументов равно .

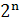Конкретную комбинацию переменных 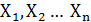называют набором.

Пример: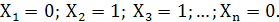

Л.Ф. называется определенной, если известно ее логическое значение для каждого возможного набора переменных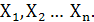

Л.Ф. называется частично определенной, если для некоторых наборов переменных 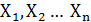функция Y = 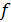( 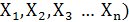недоопределена (не задана).