Построение комбинационной логической схемы по заданной функции

Имея аналитическую запись логической функции Y = 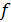( 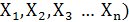, можно осуществить переход к реализации цифрового логического устройства, которое будет обрабатывать поступающие логические сигналы 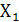, 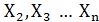по заданным требованиям.

Пример: Логическая функция представлена аналитическим выражением в совершенной дизъюнктивной нормальной форме:

Y = +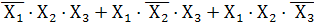

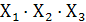
Для реализации этой логической функции потребуются:

а) инверторы (НЕ) в количестве трех штук для инвертирования , ;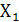

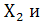
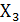б) трехвходовые конъюнкторы (И) для образования каждого из минтермов, в количестве четырех штук;

в) один дизъюнктор (ИЛИ) на четыре входа, на входы которого должны подаваться сигналы с выходов минтермов, а выход схемы ИЛИ является выходом всего устройства.

Соединив связями входы и выходы перечисленных элементов, получим логическую схему, представленную на рис. 1.1.

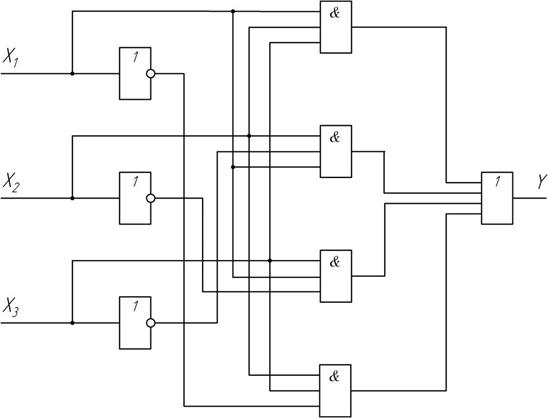
Рис. 1.1 Схемная реализация логической функции в базисе И, ИЛИ, НЕ

Таким образом, для реализации этой логической функции потребовалось 8 логических элементов. Можно показать, что реализация этой же логической функции, преобразованной в совершенную конъюнктивную нормальную форму потребует использования также 8 элементов, причем, как и в первом случае, все элементы «разномастные», что при практической реализации вызовет перерасход микросхем.

Логические базисы ИЛИ-НЕ, И-НЕ – универсальные логические функции

Элемент ИЛИ-НЕ, реализует логическую функцию вида Y = 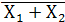(инверсия дизъюнкции). Иногда ее обозначают Y = 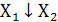(стрелка Пирса)

Условное обозначение

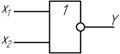
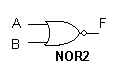
Значения функции представлены в табл. 1.5.

Таблица 1.5

Таблица истинности функции

ИЛИ-НЕ для двух аргументов

Универсальность функции может быть показана, если доказать её полноту, т.е. возможность получения трех основных логических действий в базисе И, ИЛИ, НЕ. Элемент ИЛИ-НЕ выполняет все основные логические операции:

1. операция инверсии Y = 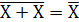. Это означает, что для получения инвертора необходимо соединить между собой все входы n-входового элемента ИЛИ-НЕ

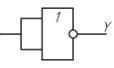
2. операция дизъюнкции Y =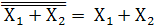

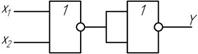
3. операция конъюнкции. Воспользуемся законом Де Моргана Y = 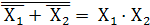, для чего аргументы Х₁ и Х₂ придется предварительно проинвертировать

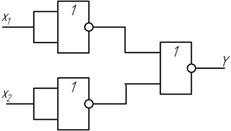
В общем случае входов может быть – «n».

Элемент И-НЕ, реализует логическую функцию вида Y = 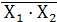(отрицание конъюнкции). Иногда ее обозначают Y = 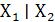(штрих Шеффера)

Условное обозначение:

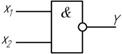
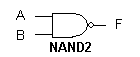
Элемент И-НЕ выполняет все основные логические операции:

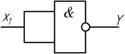
1. операция инверсии Y = 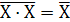, заключается в объединении всех n – входов элемента И-НЕ

2. операция конъюнкции Y =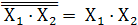

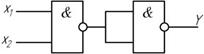
3.операция дизъюнкции может быть получена по правилу Де Моргана

Y =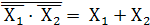

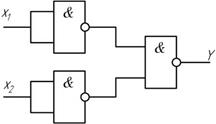
В общем случае входов может быть – «n».

Способность функций ИЛИ-НЕ и И-НЕ выражать только через самоё себя все функции Булева базиса доказывает, что эти функции обладают логической полнотой. С практической точки зрения это означает, что разработчик схем получает возможность проектирования любой сколь угодно сложной схемы с помощью одной лишь функции И-НЕ или ИЛИ-НЕ. Важным свойством функции И-НЕ оказалось и то, что именно её удалось эффективно реализовать средствами самой массовой интегральной технологии – ТТЛ. Поэтому именно микросхемы, выполняющие функцию И-НЕ уже не одно десятилетие выпускаются в самом массовом количестве, а самому элементу присвоено звание «тяговой лошадки» схемотехники малой и средней степени интеграции.