Способы представления логических функций

1 способ – словами. Например – правило выполнения операции дизъюнкции: значение функции Y истинно, если хотя бы один из ее аргументов принимает единичное значение.

2 способ – табличный с помощью таблиц истинности.

3 способ – аналитический, который в свою очередь делится на дизъюнктивную и конъюнктивную формы.

4 способ – графический, использующий геометрическое представление логической функции в виде n-мерных кубов или матриц Карно (в данном материале не излагается).

Рассмотрим пример изложения некоторой логической функции:

словами: Значение функции трех аргументов считается истинным, если хотя бы два аргумента приняли единичные значения. В остальных случаях функция Y ложна, то есть равна 0.

От словесного описания функции перейдем к её формальному выражению в виде таблицы истинности (табл. 1.4):

число строк таблицы равно 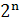, где n = 3 – число независимых аргументов, т.е.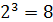

Таблица 1.4

Таблица истинности функции трех

переменных Х₁, Х₂ и Х₃

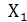
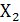
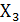
			Y

Это мажоритарный элемент (франц. – большой, большинство), т.е. необходимо наличие min 2 аргументов (большинство из трех) чтобы Y = 1.

аналитически: Анализируя вышеприведенную таблицу истинности, видим, что значение Y = 1 если:

а) 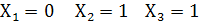т.е. сочетание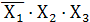

или

б) 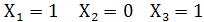т.е. сочетание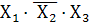

или

в) 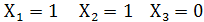т.е. сочетание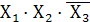

или

г) 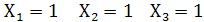т.е. сочетание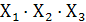

Каждое из произведений аргументов, содержащее все переменные в прямом или инверсном виде, для которых значение Y истинно или ложно называют минтермом или конституентом 1 или 0 соответственно.

Тогда логическую функцию Y = 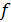( 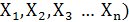можно представить в виде суммы четырех минтермов (конституентов 1).

Y = +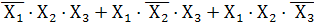

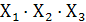
Если при такой замене каждое слагаемое функции содержит произведение всех переменных 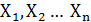или их инверсий, то функцию называют совершенной дизъюнктивной нормальной или первой стандартной формой СДНФ ( для справки, напоминаю, что минтермы, в которых нет переменных, встречающихся более одного раза, называют нормальными, а термин совершенной формы ограничивает число входящих в выражение минтермов против максимально возможного их числа, так как в противном случае их сумма превратится в 1).

Точно так же можно выделить и ложные (нулевые) значения функции (из табл.), т.е.

Значение Y = 0 если:

а) 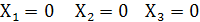т.е. сочетание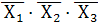

или

б) 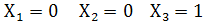т.е. сочетание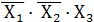

или

в) 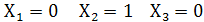т.е. сочетание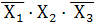

или

г) 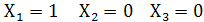т.е. сочетание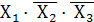

Следовательно:

= +

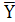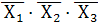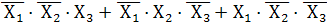
Поставив инверсии над левой и правой частями выражения и используя правило Де Моргана, получим:

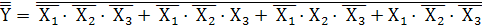
Y =(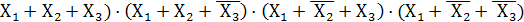

Функция в этом случае представлена в виде конъюнкции дизъюнкций переменных. Такую форму представления логической функции называют совершенной конъюнктивной нормальной или второй стандартной формой СКНФ.