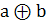Минимизация логических функций
Задача разработчика устройства или схемы не только в том, чтобы создать устройство, в принципе выполняющее заданную логическую функцию, но и в том, чтобы из всех возможных вариантов выбрать наилучший, требующий наименьшего числа элементов для реализации.
Поэтому, после получения аналитической формы записи логической функции, необходимо осуществить ее минимизацию.
Существует несколько способов минимизации логических функций: алгебраический, метод карт Карно, составление программ ЭВМ.
Пример алгебраической минимизации логической функции, заданной аналитическим способом
Дано: Y =( 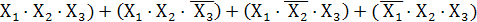
Определимся с затратами на реализацию этого выражения: три инвертора, четыре трехвходовых конъюнктора и один четырехвходовый дизъюнктор, что в сумме составляет восемь элементов ( к тому же «разномастных»), рис.1.
Решение: Прибавим (логически, конечно) к первому минтерму еще два таких же минтерма. Результат не изменится по закону тавтологии:
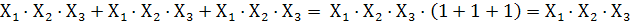
получим:
Y= 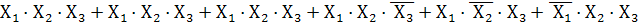 перегруппируем члены:
перегруппируем члены:
Y = 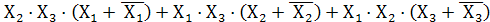
по правилу сочетания переменной с ее инверсией: 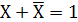
тогда: Y = 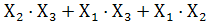
Если функция не поддается дальнейшей минимизации, то такую форму записи называют тупиковой.
Схема реализации полученного выражения представлена на рис. 1.2.
Эта схема требует уже всего 4 элемента, а не восемь: три двухвходовых элемента – И и одного трехвходового элемента – ИЛИ, однако второй недостаток – «разномастность» используемых элементов, остался.
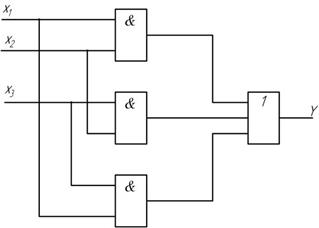
Рис. 1.2 Схема минимизированной функции
Y = 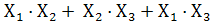
Однако разработчик должен стремиться к использованию однотипных элементов, например, универсальных элементов И-НЕ. Поэтому минимизированное выражение надо представить как отрицание конъюнкций: (по правилу Де - Моргана: инверсия дизъюнкциий есть конъюнкция инверсий). Охватим выражение двумя инверсиями и одну из инверсий израсходуем для преобразования дизъюнкции в конъюнкцию.
Y= 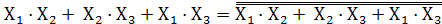 =
=
=( 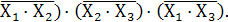
Схема реализации на элементах И-НЕ показана на рис. 1.3.
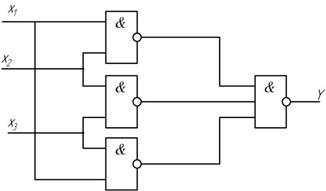
Рис. 1.3 Схема реализации задачи на элементах И-НЕ
Для реализации этой же задачи на элементах ИЛИ-НЕ поставим четыре инверсии на всем выражением.
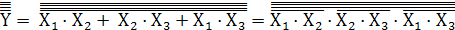 =
= 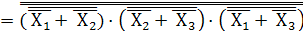
Реализация схемы на элементах ИЛИ-НЕ показана на рис. 1.4.
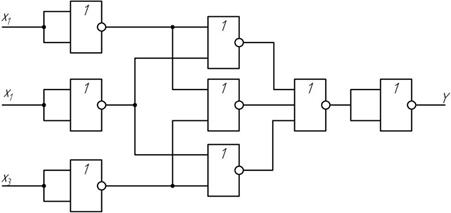
Рис. 1.4 Схема реализации задачи на элементах ИЛИ-НЕ
Сумма по модулю 2
Только в случае двух аргументов эту функцию называют функцией неравнозначности, исключающее ИЛИ. В формулах записывается как в сокращенном виде Y = a Å b, так и в развернутом Y = a×`b + `a×b. Название функции связано с тем, что a Å b есть арифметическая сумма двоичных чисел a и b в пределах одного двоичного разряда:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 =10
В последней сумме возникла единица переноса в старший разряд, а в
пределах младшего разряда сумма равна нулю.
Таблица истинности функции приведена в табл. 1.6.
Таблица 1.6
Таблица истинности функции М2
| a | b | Y |
Изображение функции М2
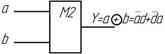
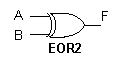
Элементы, реализующие функцию М2 применяются для построения счетных и суммирующих устройств.
На рис. 1.5 приведены схемы построения функции М2 на различных элементах
|
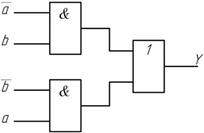 а
а
|
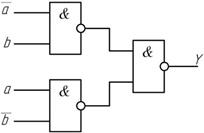 б
б
Рис. 1.5 Схемы построения М2 на элементах а – И, ИЛИ, б – И-НЕ
Свойства функции М2.
Правило: При инвертировании одного из аргументов вся функция М2 инвертируется:
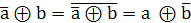
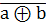 =
= 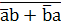 =
= 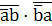 = (
= ( 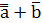 )·(
)·( 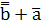 ) =
) = 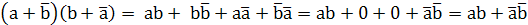
Функция Y = 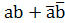 называется функцией равнозначности или тождества.
называется функцией равнозначности или тождества.
Форма записи Y = 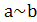 , Y =
, Y = 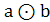 (табл. 1.7).
(табл. 1.7).
Изображение на схемах
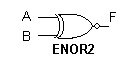
Таблица 1.7
Таблица истинности
функции равнозначности
| 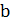
| Y |
Как видно из табл. 1.7 функция срабатывает, т.е. Y = 1 в двух случаях, в которых a = b, поэтому такой элемент является простейшим компаратором – устройством, предназначенным для сравнения цифровых кодов.
Рассмотрим правила сочетания аргумента «а» с константами 0, 1 с самим аргументом «а» и его инверсией.
Для функции М2:
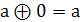
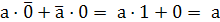
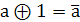
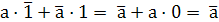
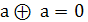
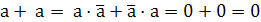
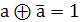
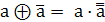 +
+ 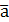
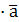 =
= 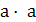 +
+ 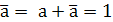
Для функции 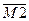 :
:
а 0 = 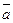
а 1 = а
а а = 1
а 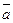 = 0
= 0
Сумматор по М2 можно построить на любое число входных аргументов.
Например, на три аргумента: Y = 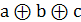 =
= 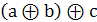 =(
=( 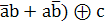 = (
= ( 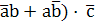 + (
+ ( 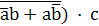 =
= 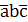 +
+ 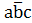 + (
+ ( 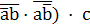 =
= 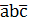 +
+ 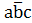 +
+ 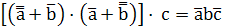 +
+ 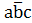 +
+ 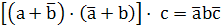 +
+ 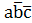 + (
+ ( 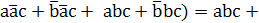
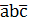 +
+ 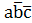 +
+ 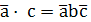 +
+ 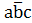 +
+ 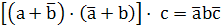 +
+ 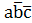 +
+
( 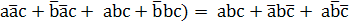 +
+ 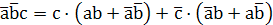
Мы рассмотрели лишь некоторые логические функции, в основном те, которые выпускаются промышленностью в конкретных сериях микросхем. Это, так сказать, костяк, основа основ логических схем. Однако из теории известно, что возможное количество логических действий над двумя переменными равно 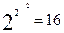 .
.
В табл. 1.8 приведены все 16 логических действий над двумя переменными. С частью этих действий мы уже познакомились, другие действия собственно действиями и не являются, т.к. представляют собой константы, третьи оказались не востребованными и для широкого практического применения в виде микросхем не выпускаются.
Таблица 1.8
Логические действия над двумя переменными
| a | b | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
Кратко перечислим все представленные в табл. 1.8 функции.
F0 = 0 и F15 = 1 – константы соответственно 0 и 1. Не имеют смысла как логические действия, включены в таблицу формально.
F3 = а и F5 = b – повторители аргументов a и b соответственно. Логического смысла не имеют, но выпускаются микросхемы, содержащие повторители, предназначенные для преобразования уровней логических сигналов, например, от ТТЛ к КМОП и наоборот.
F10 = b̅ и F12 = a̅ - инверсии аргументов b и a соответственно, также не являются логическими действиями над двумя переменными.
F1 = a · b – конъюнкция a и b.
F2 = a · b̅ - функция запрета b: сигнал на выходе появляется лишь при а = 1 и отсутствии сигнала b. Практическое применение нашла лишь в специализированных микросхемах.
F4 = ā · b – функция запрета по «а». Аналогична F2.
F6 = F2 + F4 = а·b̅ + ā·b – функция неравнозначности, она же «исключающая ИЛИ», она же М2.
F7 = a + b – дизъюнкция a и b.
F8 = F̅7 = 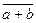 - инверсия дизъюнкции (стрелка Пирса).
- инверсия дизъюнкции (стрелка Пирса).
F9 = F̅6 = a ~ b = a·b + ā•b̅ - функция равнозначности.
F11 = F̅4 = b→a = ā̅̅̅ ̅•̅b̅ = a + b̅ – импликация (сплетение).
F13 = F̅2 = a→b = a̅•̅b̅̄ = ā + b - импликация (конверсия).
F 14 = F̅1 = a̅•̅b̅ - инверсия конъюнкции (штрих Шеффера).
Рассмотренный материал справедлив для двух аргументов. С ростом числа переменных существенно изменяются отклики таких схожих между собой функций как: М2, неравнозначность и исключающее ИЛИ.
Вот как подчеркивает неправомерность безусловного отождествления вышеназванных функций Потемкин И.С.
Составим две таблицы истинности для функций М2, неравнозначность, ИЛИ и исключающее ИЛИ, одну табл. 1.9 для двух, а другую табл. 1.10 для трех аргументов и проведем их сравнительный анализ.
Таблица 1.9
Функции двух аргументов
| b | a | M2 a⊕b (нечетность) | Неравенство (несовпадение) | Исключающее ИЛИ (один и только один) | Дизъюнкция (ИЛИ) |
Таблица 1.10
Функции трёх аргументов
| c | b | a | M2 a⊕b⊕c (нечетность) | Неравенство (несовпадение) | Исключающее ИЛИ (один и только один) | Дизъюнкция (ИЛИ) |
Как видно из табл. 1.9 при двух аргументах значения трёх первых функций полностью совпадают, что вызывает путаницу и подмену терминов. Из табл. 1.10 ясно следует, что при числе аргументов равном трем ( и более тоже) все перечисленные функции совершенно различны. Автор объясняет неоднозначность технических и даже логических терминов неоднозначностью разговорного языка, т.к. грамматика русского языка не различает функций исключающего ИЛИ и просто ИЛИ. В качестве примера автор приводит следующие выражения: Ревет ли зверь в лесу глухом, трубит ли рог, гремит ли гром,… союз «ли», являющийся краткой формой «или», имеет значение дизъюнкции, а в возгласе «Кошелёк или жизнь» тот же союз «или» выражает уже исключающее ИЛИ.
Вообще, мы сами того не замечая в повседневной жизни, конечно, используем логические выражения. Ярким примером может служить, например, басня И.А. Крылова «Лебедь, Щука и Рак» (1816).
Когда в товарищах согласья нет,
На лад их дело не пойдет,
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак да Щука
Везти с поклажей воз взялись,
И вместе трое все в него впряглись;
Из кожи лезут вон, а возу всё нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвётся в облака,
Рак пятится назад, а Щука тянет в воду…
Это длинное и красочное описание мучений героев басни легко укладывается в логическое выражение конъюнкции векторов действующих сил:
В = Л · Р · Щ, где В – движение воза, Л – лебедь, Р – рак, Щ – щука.
Понятно, что если хотя бы один персонаж будет иметь вектор отличный от общего, т.е. инверсию равную нулю, то и все произведение обратится в нуль.
Ещё пример: Это ни рыба, ни мясо. Если бы Это было рыбой ИЛИ мясом, у нас бы не возник вопрос: Что Это такое? Мы бы утверждали, что логической связкой является дизъюнкция. Однако исходное выражение отрицает причастность и к рыбе и к мясу, следовательно, мы имеем дело с инверсией дизъюнкции, а формула выражения примет вид: Э = р̅̅v̅м̅ = р̅ʌм̅, что соответствует выражению Это ни рыба И ни мясо.
\Самостоятельно определиться с выражениями:
1. За двумя зайцами погонишься – ни одного не поймаешь.
2. Читай не так как пономарь,
А с чувством, с толком, с расстановкой. А.С. Грибоедов «Горе от ума»
3. Я еду, еду, не свищу,
А как наеду, не спущу. А.С. Пушкин «Руслан и Людмила»
4. Минуй нас пуще всех печалей
И барский гнев, и барская любовь. А.С Грибоедов «Горе от ума»
5. Чем меньше женщину мы любим,
тем больше нравимся мы ей. А.С. Пушкин «Евгений Онегин»
Дата добавления: 2017-05-02; просмотров: 3833;

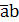 +
+ 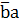 =
=