Основы Булевой алгебры
Булева алгебра была впервые описана английским математиком Чарльзом Людвигом Доджосоном, более известным под псевдонимом Льюис Кэрролл, а в 1854 году шотландский математик Джордж Буль ввел двузначную алгебраическую систему, называемую теперь булевой алгеброй. Правда, первоначально аппарат алгебры разрабатывался как средство разбора, подтверждения или, наоборот, отклонения сложных философских высказываний и лишь в 1938 году американский инженер Клод Элвуд Шеннон показал, как приспособить булеву алгебру для описания поведения и анализа схем, составленных из электромеханических реле, которые в то время были самыми распространенными логическими элементами.
Электромеханическое (электромагнитное) или просто реле при всей его громоздкости и черепашьей скорости переключений обладает несомненными достоинствами, которые заставляют и в настоящее время их производить и использовать. Первое достоинство – гальваническая развязка между цепью управления (обмоткой) реле и его контактами. Второе достоинство, имеющее отношение к алгебре логики, двоичное состояние контактов - замкнутое или разомкнутое (конечно при условии, что механика реле исправна, а сами контакты не окислены и не разболтаны).
В алгебре Буля используют двоичную переменную X, удовлетворяющую аксиомам или постулатам, т.е. утверждениям, про которые мы предполагаем, что они справедливы, и из которых вытекают все другие свойства системы.
Аксиома 1. X 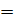 1, если X
1, если X 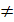 0 и X = 0, если X
0 и X = 0, если X 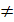 1. Другими словами - Да это Да, а Нет это Нет, контакты либо замкнуты, либо разомкнуты и т.д.).
1. Другими словами - Да это Да, а Нет это Нет, контакты либо замкнуты, либо разомкнуты и т.д.).
Аксиома 2. Если Х = 0, то Не Х = 1, если Х = 1, то Не Х = 0
Другими словами – если некое реле имеет переключающую группу и в этой группе нормально разомкнутый контакт разомкнут, то в этот же момент времени нормально замкнутый контакт того же реле замкнут.
С учетом перечисленных аксиом рассмотрим три основные простейшие логические операции: дизъюнкцию, конъюнкцию и инверсию.
Операция дизъюнкции (с латинского- разобщение). Обозначается знаками «V» или «+».Другое название этого действия: ИЛИ (операция логического сложения). Для двух переменных Х1 и Х2 эта операция даёт результаты, представленные в табл. 1.1, получившей название таблицы истинности, где представлены все возможные сочетания 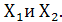
Таблица 1.1
Таблица истинности операции ИЛИ
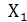
| 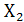
| Y |
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Вывод: Переменная Y принимает единичное значение, если хотя бы одна из переменных равна единице.
Аналитическая запись: Правильная Х1 V Х2 = Y, допускаемая Х1 + Х2 = Y Читается: Игрек равен икс один или икс два.
Переменных в общем случае может быть n, то есть 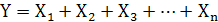 .
.
Значение 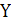 истинно, если истинна хотя бы одна из переменных
истинно, если истинна хотя бы одна из переменных 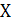 .
.
Условное обозначение ЛЭ ИЛИ – дизъюнктора
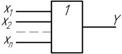
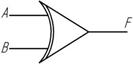 Американская
Американская
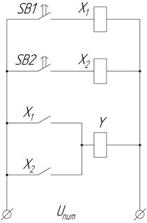
Схемная реализация логического элемента ИЛИ на контактах и реле

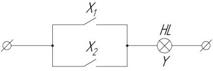
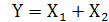
Операция конъюнкции (с лат. соединение). Другое название «И» (операция логического умножения). Записывается в виде: Правильно 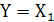 Λ
Λ 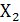 или Y = X1 & X2, допускается Y = X1 × X2 или даже совсем без точки Y = X1X2
или Y = X1 & X2, допускается Y = X1 × X2 или даже совсем без точки Y = X1X2
Читается: Игрек равен икс один И икс два.
Составим таблицу истинности (табл. 1.2) для операции конъюнкции двух переменных, в которой также перечислим все возможные сочетания значений Х1 и Х2.
Таблица 1.2
Таблица истинности операции И.
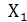
| 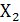
| Y |
0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1
Вывод: Переменная 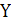 принимает единичное значение только в том случае, когда переменная
принимает единичное значение только в том случае, когда переменная 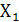 так же как переменная
так же как переменная 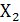 принимает единичное значение.
принимает единичное значение.
Для n переменных:
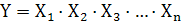
Значение 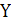 истинно, если истинны все переменные Хn.
истинно, если истинны все переменные Хn.
Условное обозначение логического элемента И – конъюнктора
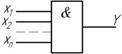
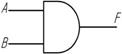 Американская
Американская
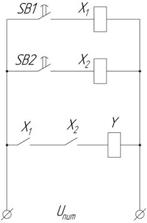
Схемная реализация логического элемента И на контактах и реле
Операция инверсии (НЕ) - операция логического отрицания
Записывается в виде 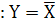
Читается: Игрек равен не икс
Так как операция выполняется над одной переменной 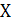 , то число возможных значений равно 21 = 2, что и отражено в таблице истинности (табл. 1.3).
, то число возможных значений равно 21 = 2, что и отражено в таблице истинности (табл. 1.3).
Таблица 1.3 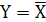
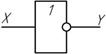
Таблица истинности
операции инверсии
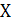
| 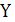
|
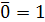
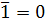
Условное обозначение инвертора
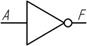 Американская
Американская
Схемная реализация на контактах и реле:
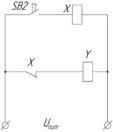
Дата добавления: 2017-05-02; просмотров: 8409;











