Формула Клапейрона-Клаузиуса

Поскольку уравнение Ван-дер-Ваальса учитывает собственный объем молекул и их взаимное притяжение на расстоянии (что проявляется в существовании фазовых переходов), то оно может быть использовано для выяснения связи температуры фазового перехода первого рода (испарение-конденсация либо плавление-отвердевание) с изменением объема при фазовом переходе и с количеством теплоты, необходимым для изменения агрегатного состояния (например, для превращения воды в пар или льда в воду).

Сначала обратим внимание на возможность изобразить работу тепловой машины через площадь фигуры цикла не только в координатах давление-объем, но и в координатах температура-энтропия. Так, например, цикл Карно в этих координатах представляется прямоугольником, поскольку обратимые адиабатные процессы являются изоэнтропными и при δQ = 0 из уравнения (5.1) следует dS = 0, и значит S = const, а изотермы изображаются прямыми линиями, перпендикулярными оси температур. На Рис.5 представлен цикл Карно в этих координатах.

T

Т₁

T₂

Т₂ 4 3

S₁ S₂ S

Рис.5. Цикл Карно в координатах энтропия-температура (S,T).

Диаграмма цикла Карно в этих координатах хорошо иллюстрирует КПД цикла. Легко понять, что количество теплоты, полученное от нагревателя при температуре T_1, выражается площадью прямоугольника между точками 1 и 2 и осью абсцисс, то есть Q₁ = T₁(S₂ – S₁). Количество теплоты, отданное холодильнику при температуре Т₂, соответственно будет равно Q₂ = T₂(S₂ – S₁). КПД цикла Карно равен отношению площадей прямоугольников (Q₁ - Q₂)/Q₁ = (T₁ - Т₂)/T_1. Площадь, ограниченная на рисунках линиями цикла 1-2-3-4, отображает то количество теплоты, которое преобразуется тепловой машиной за цикл в механическую работу, независимо от того, идет ли речь об изображении цикла в координатах давление-объем (P,V) на Рис.3 или в координатах температура-энтропия (T,S) на Рис.5. Значит, эти площади можно приравнять. Если речь идет об элементарном цикле, то фигура из двух близких адиабат и двух близких изотерм дает в координатах (P,V) параллелограмм, а в координатах (T,S) – прямоугольник, площади которых равны

dPdV = dTdS = dTdQ/T= dQ·dT/T.

В этом выражении отношение dT/T есть КПД элементарного цикла Карно, а δQ – количество полученной от нагревателя теплоты. Если применить полученную формулу к циклу, построенному на фазовом переходе, происходящем при постоянном давлении и постоянной температуре, и потом вычислить площадь цикла, проинтегрировав в первом случае по объему, а во втором по энтропии, то есть по количеству теплоты, поступающей в систему при фазовом переходе, то получим формулу

которая дает (после интегрирования) уравнение, связывающее изменение температуры фазового перехода при изменении давления в термодинамической системе с теплотой фазового перехода и изменением объема при изменении агрегатного состояния вещества, а именно уравнение Клапейрона-Клаузиуса

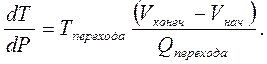(8.6)

Применение этой формулы в практически интересных случаях (например, для вычисления изменения температуры кипения воды в скороварке или температуры плавления льда под лезвием конька) рассматривается в задачах к курсу термодинамики.

8.3. Фазовые диаграммы состояния. Тройная точка

Уравнение Клапейрона-Клаузиуса (8.6) применимо к любому фазовому переходу, а не только к переходу жидкость-пар, но и к плавлению (твердое тело - жидкость) и к возгонке (твердое тело - пар). В правой части этого уравнения стоят измеримые на опыте величины, поэтому, опираясь на экспериментальные данные, можно построить на графике в координатах температура-давление (T, P) кривые равновесия вещества в разных агрегатных состояниях. Для любой пары агрегатных состояний можно построить кривые, показывающие зависимость температуры фазового перехода от давления. Если взять три агрегатных состояния, то получаются два уравнения, связывающие две независимые переменные. Решение в этом случае может существовать лишь в одной точке, то есть при вполне определенных значениях температуры и давления (T, P). Эта точка получила название тройная точки на фазовой диаграмме состояний вещества.

В качестве примера тройной точки обычно приводятся координаты тройной точки воды при давлении Р = 4,58 мм рт ст и абсолютной температуре Т = 273,16 ^оК, которая, напомним, является опорной температурой при построении термодинамической шкалы температур. В этой тройной точке сосуществуют одновременно твердая фаза (лед), жидкая фаза (вода) и газообразная фаза (пар).

Справедливости ради следует отметить, что даже однокомпонентная система (не говоря уже о многокомпонентных) может иметь более одной тройной точки вследствие возможности существования различных модификаций состояния вещества. Это действительно имеет место при перестройке кристаллической структуры твердых веществ. На Рис.6 представлены кривые равновесия фаз чистого вещества (воды) вблизи 0^оС. Кривая кипения показывает ход давления насыщенного пара с ростом температуры.

Р

кривая плавления критическая точка 4,58 тройная точка

мм.рт.ст. лёд кривая пар

возгонки

273,16 К Т

Рис.6. Кривые равновесия фаз чистой воды.

Фазовая диаграмма воды демонстрирует свойство, которое термодинамически хотя и не запрещено, однако является довольно необычным для природных веществ, а именно, одна из кривых равновесия фаз (вода-лед) имеет отрицательный наклон, что связано с увеличением объема при превращении воды в лед (лед, как известно, плавает в воде, а, например, оливковое масло при замерзании с поверхности опускается на дно сосуда хлопьями). Обычно удельный объем вещества в жидком состоянии больше, чем в твердом (хотя аномально в этом отношении и аналогично воде ведет себя чугун, что весьма удобно при использовании чугуна для художественных отливок, так как чугун хорошо заполняет подробности рельефа литейной формы). Отрицательный наклон кривой плавления льда имеет значение для катания на коньках – лед плавится под уголком лезвия конька (при хорошей заточке, естественно), и конек, заглубляясь в лед, позволяет отталкиваться от льда. Знание из опыта удельной теплоты плавления льда и изменения удельного объема при фазовом переходе позволяет через уравнение Клапейрона-Клаузиуса количественно достаточно точно просчитать это явление.

Существование критической точки позволяет перейти из области пара в область жидкости без видимого фазового перехода, но эта возможность уже была видна при рассмотрении изотерм газа Ван-дер-Ваальса.

При фазовых переходах первого рода имеет место поглощение (выделение) теплоты фазового перехода. Это происходит при плавлении, испарении, возгонке и при переходе кристаллических тел из одной кристаллической формы в другую (например, переход серы из ромбической формы в моноклинную при 369⁰К, с последующим плавлением при 393^оК).

Следует, для общности, упомянуть о существовании фазовых переходов второго рода, при которых нет поглощения (выделения) теплоты перехода и нет изменения удельного объема, но в точке фазового перехода скачком меняются теплоемкость, коэффициент температурного расширения и сжимаемость, то есть изменяются вторые производные от термодинамических потенциалов. Примером фазовых переходов второго рода может служить точка Кюри – температура, при которой ферромагнетик теряет свои ферромагнитные свойства и превращается в обычный парамагнетик (например, для железа эта температура равна 1043⁰ К).

9. КРИТЕРИИ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ

9.1. Тепловое равновесие и неравенство Клаузиуса

Как уже отмечалось ранее, полученные в классической феноменологической термодинамике («термостатике») связи между термодинамическими величинами относятся к состояниям термодинамического равновесия или весьма близким к ним (пренебрежимо мало отличающимся от равновесных). Что же касается процессов перехода к состоянию теплового равновесия, то о них до сих пор говорилось только, что изолированная (полностью отключенная от всех внешних влияний) термодинамическая система сама собой идет к состоянию термодинамического равновесия, то есть к выравниванию по всему объему всех интенсивных термодинамических характеристик. Этот опытный факт зафиксирован в той части содержания второго начала термодинамики, которая утверждает, что энтропия любой изолированной термодинамической системы стремится к максимуму.

Этот критерий термодинамического равновесия (максимальность энтропии) связан с выполнением довольно неудобных для практических приложений условий. Действительно, стремление энтропии к максимуму при приближении термодинамической системы к равновесному состоянию справедливо только для изолированных систем, что, конечно, отнюдь не всегда осуществляется на практике, и, следовательно, этот критерий равновесия для практики не всегда удобен. Поэтому необходимо рассмотреть критерии равновесия для неизолированных термодинамических систем и найти другие (не энтропию) функции состояния термодинамической системы, которые будут стремиться к экстремуму при самопроизвольном переходе к равновесному состоянию термодинамических систем в условиях неизолированности, то есть в условиях наличия силовых, тепловых и вещественных контактов систем с внешними телами.

Неравновесность накладывает определенные ограничения. В феноменологической термодинамике термодинамические функции состояния, уравнения состояния (термические и термодинамические) и даже некоторые термодинамические параметры (например, температура) определены, то есть имеют смысл, только для систем, находящихся в равновесном состоянии. Поэтому следует особо отметить, о чем может идти речь, когда обсуждается состояние системы, не находящейся в состоянии равновесия, а лишь приближающейся к этому состоянию. То есть, следует определиться с пониманием того, что подразумевается под параметрами и функциями состояния в условиях некоторого отклонения от состояния равновесия, а именно, определиться с тем, что мы понимаем под вариациями функций и параметров. Под этим надлежит понимать такие процедуры, выполняемые с термодинамическими системами, при которых на функции и параметры накладываются определенные ограничения. А именно, мы будем считать, что рассматриваемую термодинамическую систему всегда можно разделить на квазиизолированные друг от друга области (то есть, энергия взаимодействия частей системы много меньше энергии каждой из частей). В таких случаях термодинамические состояния в подсистемах можно рассматривать как независимые друг от друга и равновесные (небольшие подсистемы быстрее приходят в состояние равновесия, чем вся система). При этом аддитивные функции состояния (например, энергия или энтропия) могут считаться равными сумме функций, найденных для равновесных частей, хотя, конечно, их значения могут отличаться от тех значений, которые они имели бы при установлении общего равновесия во всей системе.

Для получения общих условий равновесия в термодинамических системах воспользуемся неравенством Клаузиуса (5.6), соединяющим в себе первое и второе начало термодинамики (где нас будет интересовать самопроизвольное стремление энтропии к максимуму при стремлении термодинамической системы к равновесию)

TdS > dU + PdV .

Далее мы будем рассматривать гипотетические вариации функций состояния системы, выводящие систему из состояния равновесия. В таких случаях возвратный переход системы при восстановлении равновесия, как полагается, необратим, но для самих таких гипотетических вариаций неравенство Клаузиуса (в результате изменения знаков) дает выражение

- TdS > - ( dU + PdV) ,

которое превращается в базовое уравнение для выяснения общих условий равновесия

dU + PdV - TdS > 0. (9.1)

Это уравнение есть общее неравенство для вариаций в термодинамических системах. Еще раз подчеркнем, что знак этого неравенства противоположен знаку неравенства Клаузиуса, поскольку здесь речь идет не о действительных изменениях, приводящих систему в равновесие, а о гипотетических вариациях, выводящих систему из состояния термодинамического равновесия.

Эти мысленные эксперименты с термодинамическими системами необходимы нам, чтобы понять, как поведут себя различные функции состояния при небольших отклонениях от равновесия. То есть мы рассматриваем здесь, что стало бы с интересующими нас функциями, если бы система сама собой немного отклонилась от равновесного состояния.