Системы с механической связью

Рассмотрим, что нового вносит в условия равновесия термодинамических систем хороший теплообмен с окружающими телами, когда температура термодинамической системы все время успевает сравняться с температурой окружающей среды. Наиболее важным для практики является, конечно, случай изотермических процессов, идущих в условиях, близких к равновесным процессам.

Если, наряду с температурой, неизменным оказывается также объем системы (dV = 0), то общее неравенство для вариаций (9.1) с учетом постоянства температуры дает выражение d(U - ТS) > 0. Поскольку функция состояния термодинамической системы, именуемая свободной энергией есть F = U - ТS , то для систем с хорошим теплообменом (Т = const.) и при постоянстве объема условие термодинамического равновесия принимает вид

(dF)_Т,V > 0. (9.5)

Аналогичным образом из общего неравенства для вариаций (9.1) можно получить условие изотермического равновесия при постоянном давлении, что выразится в требовании минимальности термодинамического потенциала Гиббса G = U + PV – TS, то есть в виде

(dG) _Т,Р > 0. (9.6)

Напомним еще раз, что в условиях равновесных (обратимых) процессов все эти функции (внутренняя энергия, энтальпия, свободная энергия и потенциал Гиббса) играют роль, аналогичную роли потенциальной энергии в механике. Подобно потенциальной энергии в механике все эти функции минимальны, когда система находится в состоянии теплового равновесия, и следовательно, любое выведение системы из этого состояния связано с затратой работы внешних сил.

.

9.3. Реакция термодинамической системы на внешнее воздействие. Принцип Ле-Шателье-Брауна

Принцип Ле-Шателье-Брауна предсказывает направление процессов, которые будут протекать в термодинамической системе, при выведении системы внешним воздействием из устойчивого равновесного состояния, хотя этот принцип зачастую не позволяет сделать сколько-нибудь точных количественных заключений.

Исторически принцип Ле-Шателье-Брауна был получен из аналогии с законом индукции Ленца: При изменении магнитного потока сквозь проводящий электрический контур в этом контуре возникает ток, такой по величине и направлению, что он своим магнитным полем стремится компенсировать то изменение магнитного потока, которым он вызывается.

Принцип Ле-Шателье-Брауна утверждает, что всякое внешнее воздействие вызывает в равновесной термодинамической системе такие побочные процессы, которые стремятся ослабить прямой результат этого внешнего воздействия. То есть, когда термодинамическая система испытывает внешнее воздействие, изменяющее непосредственно один из параметров, характеризующих состояние системы, то другой параметр, прямо не связанный с этим внешним воздействием, меняется таким образом, чтобы затруднить изменение первого параметра. Так, например, если внезапно увеличить давление извне на термодинамическую систему, то первое время, пока процесс сжатия происходит практически адиабатно, сжатию противодействует не только уменьшение объема и прямо связанное с ним повышение давления, но и повышение температуры как результат адиабатного сжатия. Здесь побочный эффект – повышение температуры - препятствует прямому эффекту внешнего воздействия – уменьшению объема, поскольку повышение температуры вызывает повышение давления внутри системы и сжимать систему становится труднее. Таким образом, принцип Ле-Шателье-Брауна утверждает, что внешнее воздействие, выводящее термодинамическую систему из состояния устойчивого равновесия, провоцирует в этой системе процессы такого направления, что они стремятся воспрепятствовать изменениям в системе, вызываемым этим внешним воздействием.

Итак, равновесие термодинамической системы, подвергшейся внешнему воздействию, смещается в таком направлении, чтобы по возможности скомпенсировать результат внешнего воздействия.

Практическая ценность принципа Ле-Шателье-Брауна состоит в том, что он позволяет без конкретного анализа предсказывать направление, в котором будут изменяться термодинамические характеристики равновесной системы, подвергшейся внешнему воздействию.

Этот принцип оказался удобен для выяснения, в каком направлении смещается состояние равновесия сложной, многокомпонентной системы в случаях, когда детальный анализ затруднителен. Особенно полезным этот принцип оказался в применении к химическим реакциям. Так, если химическая реакция эндотермическая, то есть протекает с поглощением теплоты, то нагревание системы ведет к возрастанию выхода продуктов реакции, и наоборот, если реакция экзотермическая (с выделением теплоты), то нагревание системы ведет к уменьшению выхода продуктов реакции. Понятно, что знание такого поведения химических реакций чрезвычайно полезно для практики, так как позволяет в зависимости от потребности усилить или уменьшить эффект внешнего воздействия.

10. ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ

10.1. Связь термодинамики и статистической физики. Термодинамическая вероятность (статистический вес) состояния системы и энтропия

Ранее уже упоминалось, что с точки зрения механики описание состояния термодинамической системы через указание значений термодинамических параметров является неполным, так как для полного описания следует указать значения координат и импульсов всех частиц, составляющих термодинамическую систему. Понятно, что для всех частиц системы (при их числе порядка числа Авогадро) это требование невыполнимо. Однако можно найти какая часть (какая доля) всех частиц имеет координаты и импульсы, лежащие в интересующих нас пределах. Этим занимается статистическая механика, задачей которой является нахождение функции распределения частиц по координатам и импульсам, часто именуемой плотностью вероятности (хотя в математике функцией распределения называется функция, производная от которой и есть плотность вероятности). Эта функция показывает вероятность того, что частица имеет координаты и импульсы вблизи определенных значений. Хотя координаты и импульсы отдельных частиц системы все время изменяются в результате взаимодействий (столкновений), но в условиях термодинамического равновесия функция распределения частиц по координатам и импульсам с течением времени не изменяется. Это распределение при равновесном состоянии системы остается неизменным потому, что, несмотря на постоянное изменение каждой частицей ее положения в фазовом (координатно-импульсном) пространстве, все время происходит замещение одних частиц в фазовом пространстве другими, то есть тепловое равновесие в термодинамической системе носит динамический характер. Если состояние системы первоначально не было равновесным, то функция распределения частиц по координатам и импульсам со временем эволюционирует (процесс релаксации) к равновесному распределению, которое со временем уже очень редко испытывает заметные на макроскопическом уровне самопроизвольные отклонения (флуктуации) от распределения, соответствующего полностью равновесному.

Может возникнуть вопрос, откуда берется необратимость, если все микропроцессы обратимы (согласно принципу микроскопической обратимости)? Ответ следующий. Необратимость релаксационных процессов порождается статистическим характером макроскопически наблюдаемых явлений и вероятностным характером соответствующих им закономерностей. Одно и то же с макроскопической точки зрения состояние (та же самая функция распределения) может быть осуществлено большим числом различных микросостояний. Так, если две частицы обменялись местами в фазовом пространстве (обменялись энергиями), то это уже другое микросостояние, но с макроскопической точки зрения ничего не изменилось – сохранилось распределение частиц по фазовому пространству.

Число микроскопически различных способов W, осуществляющих одно и то же макросостояние, получило в статистической механике название термодинамической вероятности или статистического веса этого макросостояния. Для нахождения этого числа используется раздел математики, именуемый комбинаторикой. Так, например, число микроскопических способов такого распределения N молекул газа по объему, чтобы в одной половине объема оказались n молекул, а в другой остальные (N – n), находится согласно правилам комбинаторики по формуле для числа сочетаний из N по n, то есть

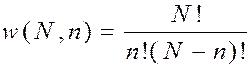
Эта функция, очевидно, имеет максимум при n = N/2, поскольку в этом случае также и (N – n) = N/2, а когда система отклоняется от этого равнораспределения, то, хотя в знаменателе (при постоянном числителе) один из сомножителей уменьшается, зато другой сомножитель увеличивается, и при этом в большей степени. Так, например, при отклонении на единицу числа молекул n от равнораспределения в знаменателе пропадает множитель N/2, но зато появляется (N/2 + 1), и в целом термодинамическая вероятность W(N,n) (статистический вес) уменьшается, и тем сильнее, чем больше отклонение от равнораспределения.

Все микросостояния системы при сохранении энергии системы равновероятны, то есть система пребывает в каждом из них одинаковое (хотя и очень маленькое с нашей, макроскопической точки зрения) время. Это предполагается в статистической механике. Поэтому вероятность приблизительно равномерного заполнения объема молекулами (при большом числе молекул) подавляюще велика по сравнению с тем, чтобы малая доля молекул оказалась в одной половине объема, а все остальные – в другой. Если искусственно создать неравномерность распределения молекул газа по занимаемому им объему, то такая система, будучи предоставлена себе самой, через некоторое время самопроизвольно придет к равнораспределению молекул по объему (выравнивание концентраций). Точно так же и температура, если она была сначала различной в разных частях системы, со временем выравнивается по всему объему.

Теперь вспомним, что в изолированной термодинамической системе энтропия самопроизвольно возрастает и остается постоянной при достижении максимума, то есть (см. (5.5))

где знак равенства относится к обратимым процессам.

В способности энтропии самопроизвольно возрастать есть нечто чуждое нашей интуиции, воспитанной на механических представлениях. Действительно, почти все законы механики (кроме связанных с трением, но это уже не вполне механика), а также оптики и отчасти электромагнетизма, обратимы во времени (почему так легко и воспринимается нами принцип микроскопической обратимости).

Для объяснения необратимости макроскопических явлений австрийский физик Людвиг Больцман в 1872 году ввел в теорию теплоты статистические представления (которые уже отчасти использовались ранее Максвеллом при рассмотрении распределения молекул газа по скоростям). Больцман предложил каждому макроскопическому состоянию приписывать статистический вес (позднее названный Планком термодинамической вероятностью), равный числу различных механических состояний микрочастиц (образующих термодинамическую систему), отвечающих одному и тому же набору значений термодинамических параметров, определяющих в термодинамике, как известно, макроскопическое состояние термодинамической системы. При таком подходе возрастание энтропии в предоставленной себе самой термодинамической системе просто означает переход в такие состояния, термодинамические вероятности которых больше. И так должно продолжаться до тех пор, пока не будет достигнуто наиболее вероятное состояние, соответствующее максимальной энтропии. Вблизи этого состояния система и будет находиться неопределенно долгое время, испытывая иногда самопроизвольные случайные отклонения от равновесия (флуктуации), теория которых рассматривается в статистической механике, а в феноменологической термодинамике флуктуациями просто пренебрегают.

Таким образом, возрастание энтропии не является абсолютным законом в термодинамике (хотя в статистической механике это обосновывается неустойчивостью решений уравнений движения микрочастиц).

Больцман предположил следующую связь между энтропией и термодинамической вероятностью

S = k^.lnW, (10.1)

где k – постоянная, получившая позднее название постоянной Больцмана.

Формула (10.1) явно соответствует всем требованиям, предъявляемым к энтропии. Энтропия функция аддитивная (как и все функции состояния), то есть энтропия системы равна сумме энтропий подсистем, S = S_A + S_B, а вероятность состояния системы (согласно теории вероятностей) равна произведению вероятностей, относящихся к подсистемам А и В, что означает W = W_A·W_B. Этому требованию удовлетворяет логарифмический характер функции (10.1). Отвечает она также требованию монотонного возрастания с ростом термодинамической вероятности.

Коэффициент k, входящий в формулу Больцмана, как величину универсальную, можно вычислить, если применить эту формулу к конкретной термодинамической системе.

Воспользуемся для этого, как обычно, моделью идеального газа.

Отношение вероятностей нахождения одной молекулы газа в объемах V₁ и V₂ (в силу хаотичности движения молекулы и, следовательно, равной вероятности нахождения в одинаковых объемах) равно отношению этих объемов, то есть

В силу теоремы о произведении вероятностей независимых событий, отношение вероятностей нахождения в объемах V₂ и V₁ всех N молекул газа равно

Поскольку согласно формуле Больцмана (10.1) изменение энтропии определяется отношением термодинамических вероятностей, то для одного моля идеального газа имеем

где N_A - число Авогадро.

Теперь вычислим изменение энтропии одного моля идеального газа в обратимом изотермическом процессе по формуле Клаузиуса (5.1), используя уравнение состояния идеального газа (3.1) PV = RT и неизменность внутренней энергии при сохранении температуры, то есть δQ = PdV,

Из сравнения полученных двумя способами изменений энтропии обнаруживаем, что

R = k N_A . (10.2)

Зная число Авогадро, легко вычислить коэффициент k в формуле Больцмана (10.1): k = 1,38·10^-23 Дж/^оК. Он является также переводным коэффициентом между единицами температуры, выраженными в джоулях, и единицами, выраженными в градусах Кельвина.