Необходимость новой функции состояния

Рассмотрение цикла Карно показывает, что даже самая совершенная, обратимо работающая тепловая машина не может за цикл превратить в работу всю взятую у нагревателя теплоту, и вынуждена часть ее отдавать холодильнику. При этом уменьшается возможность последующего преобразования теплоты в работу, потому что для такого преобразования необходима разность температур (именно она определяет КПД цикла), а она в замкнутой системе с каждым циклом будет уменьшаться. В изолированной от любых внешних связей системе с каждым циклом температура холодильника будет повышаться (а температура нагревателя понижаться), и при полном выравнивании температур нагревателя и холодильника возможность преобразования теплоты в работу будет полностью утрачена.

Невозможность полностью превратить теплоту в работу ведет к недостижимости в замкнутой системе абсолютного нуля температуры. Недостижимость абсолютного нуля в замкнутой термодинамической системе может быть принята в качестве одного из постулатов феноменологической термодинамики.

Таким образом, принципиально новым (по сравнению с механикой) свойством, обнаруживающимся уже при рассмотрении обратимых термодинамических процессов, оказывается не полная, а лишь частичная превращаемость теплоты в работу за цикл. Обнаруженное новое свойство термодинамических систем можно сформулировать, как невозможность в изолированной системе полностью избавиться от хаотического движения микрочастиц, преобразовав его все в упорядоченное движение.

Итак, в замкнутой системе нельзя полностью избавиться от тепловой, хаотической формы движения, преобразовав все движение частиц системы в упорядоченное движение.

Существует несколько эквивалентных по своему содержанию формулировок ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ (как принято называть то свойство термодинамических систем, которое означает неуничтожимость тепловой формы движения в замкнутой системе).

Одна из формулировок принадлежит Клаузиусу: «Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому телу». Эта формулировка неявно предполагает, что при этом не происходит никаких изменений в состоянии других тел. Очевидно, что если бы можно было без затраты работы передавать теплоту от холодильника к нагревателю, то не было бы никаких ограничений на полное преобразование теплоты в работу.

Объединенная формулировка Планка-Томсона утверждает, что «невозможно создать такую периодически работающую машину, которая только совершает работу за счет охлаждения резервуара тепла, но не оказывает при этом никакого иного воздействия». Здесь имеется в виду тепловая машина с нагревателем, но без холодильника. Такую тепловую машину принято называть вечным двигателем второго рода. Его существование означало бы полную превращаемость хаотической формы движения в упорядоченную просто за счет охлаждения теплового резервуара (например, мирового океана). Но «невозможен вечный двигатель второго рода» (еще одна формулировка второго начала термодинамики).

Итак, рассмотрение цикла Карно показывает, что невозможно создать тепловую машину, циклически преобразующую теплоту в работу, которая бы всю взятую из резервуара теплоту полностью преобразовывала в работу, не оказывая никакого иного воздействия.

Первое начало термодинамики утверждает неуничтожимость движения как такового. Это описывается количественно через сохранение энергии как скалярной меры движения в явной (макроскопически-кинетической) либо скрытой (потенциальной или молекулярно-кинетической) форме.

Второе начало утверждает принципиальную неустранимость в изолированной системе тепловой, хаотической формы движения. Именно принципиальную, так как частичная возможность преобразования теплоты в работу имеется до тех пор, пока в системе существует разность температур (точнее, пока в системе не наступило тепловое равновесие с выравниванием всех интенсивных параметров).

Поскольку сформулировано новое свойство, характерное для термодинамических систем, а именно принципиальная неустранимость хаотического движения микрочастиц в замкнутой системе, то становится очевидной необходимость ввести величину, количественно характеризующую эту неустранимую хаотичность. Иными словами, дальнейшее изучение второго начала требует научиться измерять в замкнутой термодинамической системе хаотичность состояния этой системы. Это означает, что для количественного определения степени хаотичности состояния термодинамической системы необходима новая функция.

5.2. Энтропия как мера хаотичности состояния термодинамической системы. Формула Клаузиуса для вычисления изменения энтропии в обратимом процессе. Термодинамическое тождество

Новое свойство требует введения нового понятия, позволяющего качественно и количественно охарактеризовать это свойство, и, естественно, новой терминологии. Клаузиус назвал (1865) величину, измеряющую степень хаотичности состояния термодинамической системы, энтропией.

Что должна представлять собой эта величина и функцией чего она должна являться? Как измерить молекулярный беспорядок (хаос)? Как энтропия выражает степень хаотичности состояния термодинамической системы?

Обратимся опять к модели идеального газа, чтобы понять, в чем проявляется и при каких изменениях параметров изменяется согласованность (корреляция) в состояниях отдельных частиц термодинамической системы.

В механической теории теплоты (которая считает справедливыми в микромире законы классической механики) состояние термодинамической системы полностью определяется координатами и импульсами всех частиц, образующих термодинамическую систему, а хаотичность состояния системы проявляется в существовании дисперсии (квадрата среднеквадратичного отклонения от среднего значения) микропараметров, определяющих состояние термодинамической системы. Дисперсия является мерой рассеяния случайных величин, а корень квадратный из дисперсии (стандарт случайной величины) дает среднеквадратичное отклонение случайной величины от ее среднего значения. При хаотическом движении микрочастиц их координаты и импульсы рассматриваются как случайные величины. Следовательно, изменение степени хаотичности состояния должно сопровождаться изменением дисперсии этих параметров (и соответственно, их стандарта – корня квадратного из дисперсии).

Модель идеального газа позволяет понять, о чем идет речь. Здесь частицы, участвующие в тепловом движении, хотя и двигаются вполне хаотически, проявляют, тем не менее, некоторую корреляцию (соответствие) своих состояний, так как существует некоторая согласованность в их движениях (импульсах) и некоторая упорядоченность расположения в пространстве (координатах). При термодинамическом равновесии сохраняется средний разброс импульсов около их среднего значения и разброс около среднего положения в пространстве (определяемый размерами сосуда с газом). Исторически сложилось так, что в термодинамике начали искать функцию, измеряющую не согласованность (корреляцию) состояний микрочастиц, а противоположную по смыслу функцию, измеряющую несогласованность микросостояний. Если под хаотичностью состояния понимать некоррелированность (несогласованность) состояний отдельных частиц термодинамической системы, то можно ввести величину, являющуюся мерой этой хаотичности и позволяющую количественно оценивать степень несогласованности состояний отдельных частиц системы, то есть степень хаотичности состояния системы (или, по крайней мере, ее изменение при изменении состояния системы). Разумеется, способы вычисления этой величины должны быть разными в феноменологической термодинамике и в статистической механике. Так в статистической механике эта функция состояния системы (мера статистически усредненного отклонения отдельных частиц системы от их усредненных положений в фазовом пространстве) вычисляется методами теории вероятностей.

Из рассмотренного примера с идеальным газом видно, что, поскольку хаотичность состояния термодинамической системы определяется независимым образом, как дисперсией координат, так и дисперсией импульсов частиц, то возможны такие изменения состояния системы, при которых величина, характеризующая степень хаотичности состояния системы, остается неизменной. Поскольку ее возрастание, например, за счет увеличения объема (увеличение дисперсии координат), может компенсироваться убыванием за счет уменьшения дисперсии импульсов при понижении температуры. Таково адиабатное расширение и сжатие газа (см. ПРИЛОЖЕНИЕ 3).

Если абсолютизировать модель идеального газа, то она позволяет также предсказать (по крайней мере, качественно) поведение искомой величины при изменении температуры. В силу самой модели идеального газа, очевидно, что его молекулы при абсолютном нуле температуры должны иметь неизменные, фиксированные координаты («упасть на дно сосуда» при внешнем силовом поле) и одинаковые, равные нулю импульсы. Это соответствует минимально возможным дисперсиям координат и импульсов и, значит, минимальному значению искомой функции. При повышении температуры дисперсия координат молекул идеального газа будет определяться только размерами сосуда (вне зависимости от температуры), а что касается дисперсии импульсов, то в рамках феноменологической термодинамики достаточно качественного указания на ее увеличение с ростом температуры (что очевидно, если мысленно повышать температуру системы, начиная с абсолютного нуля). Возможность точных количественных расчетов должны дать методы статистической механики.

При изучении новых явлений большую роль всегда играло знание величин, сохраняющихся в процессах, происходящих в изолированных системах. Огромное значение для развития механики и электричества имело открытие законов сохранения энергии, импульса и момента импульса. Поэтому естественно, что усилия исследователей тепловых закономерностей были направлены на обнаружение величин, сохраняющихся в термодинамических процессах, хотя качественное отличие термодинамики от механики очевидно: Процессы, в которых присутствует самопроизвольное выравнивание термодинамических параметров, обладают свойством необратимости, в то время как все чисто механические (без участия сил трения) процессы полностью обратимы.

Поскольку в термодинамике, наряду с необратимыми процессами, в принципе возможны также и обратимые процессы, то поиск функции, позволяющей измерить степень хаотичности состояния термодинамической системы, естественно начать с рассмотрения полностью обратимых процессов в изолированных системах. В силу полной обратимости процессов и замкнутости систем степень хаотичности состояния таких систем не должна изменяться, и, следовательно, надо искать функцию, сохраняющуюся в замкнутых системах при всех обратимых тепловых процессах (в том числе при преобразованиях теплоты в работу). Это означает, что изменение этой функции у любого из тел, включенных в замкнутую систему, должно компенсироваться равным по величине, но противоположным по знаку суммарным изменением этой функции у других тел этой изолированной системы.

По своему смыслу искомая функция должна быть функцией состояния системы. В противном случае, проводя циклически (в нужном направлении цикла) термодинамическую систему в начальное состояние с другим, меньшим значением этой функции, можно было бы, многократно повторяя цикл, свести к нулю хаотичность состояния, что противоречит невозможности всю теплоту преобразовать в работу. Следовательно, в циклических процессах, при возвращении термодинамической системы в первоначальное состояние (вне зависимости от пути возвращения и даже без требования замкнутости системы и обратимости процессов) полное изменение этой функции должно быть равно нулю.

Поиск функции состояния термодинамической системы, сохраняющейся в обратимых процессах в замкнутых (полностью изолированных от любых внешних воздействий) термодинамических системах, привел немецкого физика Рудольфа Клаузиуса к величине, первоначально получившей название «приведенная теплота». Понять, что это такое, можно из рассмотрения рабочего цикла все той же идеальной тепловой машины Карно.

Обратим внимание, что все сохраняющиеся величины носят экстенсивный характер, но сразу отметим, что ранее рассмотренная экстенсивная величина, характеризующая тепловые процессы, то есть теплота, передаваемая рабочему телу в цикле Карно, явным образом не сохраняется, несмотря на обратимость всех этапов цикла.

У нас уже есть соотношение (4.4): Q₁/Q₂ = T₁/T₂, утверждающее равенство отношения теплоты, полученной от нагревателя, к теплоте, отданной холодильнику, отношению температур нагревателя и холодильника. Уравнение можно переписать в виде отношения

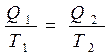
или, учитывая различия знаков для теплоты, получаемой или отдаваемой рабочим телом, Q₁/T₁ = - Q₂/T₂ , что может быть записано как Q₁/T₁ + Q₂/T₂ = 0.

Отношение переданной телу теплоты к его температуре получило первоначально название приведенной теплоты.

Уравнение

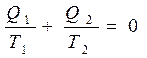
означает сохранение приведенной теплоты в цикле Карно.

Дифференциальная форма (для предельно малого цикла Карно) дает соответственно

δQ₁/T₁ + δQ₂/T₂ = 0.

Таким образом, рассмотрение цикла Карно показало, что в циклическом процессе сохраняется сумма «приведенных теплот».

Кроме того, поскольку искомая функция должна быть функцией состояния и принимать прежнее значение при завершении цикла, то ее малое изменение должно быть полным дифференциалом (математическое требование, чтобы интеграл от такого дифференциала по замкнутому пути давал нуль). Малое количество теплоты dQ полным дифференциалом не является, так как зависит от вида процесса, в котором совершается передача теплоты. Для получения из dQ полного дифференциала следует воспользоваться известной в математике процедурой нахождения интегрирующего множителя. Сохранение приведенной теплоты подсказывает, что таким множителем может быть обратная абсолютная температура. Первое начало термодинамики (2.2) dQ = dU + dA для газа в форме dQ = C_vdT + РdV и уравнение состояния идеального газа РV = RT позволяют убедиться, что это действительно так, что dQ/Т является полным дифференциалом, так как очевидно,

что справа стоит полный дифференциал функции двух переменных.

Гениальность Клаузиуса проявилась в том, что он увидел связь между изменением искомой функции состояния (изменением энтропии S) и поступлением в термодинамическую систему теплоты (то есть энергии, передаваемой через хаотическое движение микрочастиц). По Клаузиусу, это изменение определяется дифференциальным соотношением

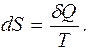(5.1)

Здесь принципиально важна обратимость процесса передачи теплоты.

Из этого соотношения сразу следует, что в обратимых процессах без теплообмена с внешними телами энтропия сохраняется (система не обязательно изолирована и может обмениваться энергией с окружением, но через работу). Так, например, обратимое адиабатное расширение или сжатие газа изоэнтропно, и степень хаотичности состояния системы сохраняется.

Возможность (по крайней мере, теоретическая) переводить систему из одного состояния в другое состояние обратимым способом через передачу теплоты (например, в квазистатическом процессе) имеет принципиальное значение, так как позволяет вычислять разность значений энтропии между двумя любыми состояниями термодинамической системы посредством интегрирования дифференциала поступающей в систему приведенной теплоты (дифференциала энтропии) по формуле

Этот прием вычисления изменения энтропии обладает всеобщностью, универсальностью, так как не связан с реально осуществляемым путем перехода системы из одного равновесного состояния в другое. Это так потому, что хотя разность энтропий находится через вычисления, относящиеся к обратимому, идеализированному переходу, но сама система может переходить из одного равновесного (начального) в другое равновесное (конечное) состояние любым (в том числе самопроизвольным и, следовательно, необратимым) способом.

Возможность написать в обобщенном законе сохранения энергии (2.2) теплоту dQ через дифференциал энтропии как TdS позволяет представить первое начало термодинамики выражением

ТdS = dU + dA, (5.3)

получившим название термодинамическое тождество, которое записывается для газообразных тел в виде

TdS = С_VdT + PdV. (5.4)

5.3. Энтропия в замкнутых системах. Обратимость процессов как условие сохранения энтропии. Энтропия и необратимость. Неравенство Клаузиуса

Для пояснения связи энтропии с неполной преобразуемостью теплоты в работу обратимся снова к циклу Карно, используя целесообразную в данном случае дифференциальную форму записи. Поскольку никаких потерь в машине Карно нет, то полученную за цикл от машины работу можно представить как разность теплоты, полученной рабочим телом от нагревателя, и теплоты, отданной рабочим телом холодильнику, то есть dA = dQ_н - dQ_х. Теперь воспользуемся выражением для коэффициента полезного действия машины Карно (4.1) h = dA/dQ_н = 1 - dQ_х/dQ_н = 1 - Т_х/Т_н. Откуда dQ_х/dQ_н = Т_х/Т_н. При передаче теплоты рабочему телу в изотермическом процессе равны температуры нагревателя и рабочего тела Т_н = Т_рт и, соответственно, равны отданная нагревателем теплота и теплота, полученная рабочим телом, dQ_н = dQ_рт. Теперь, используя выражение (5.1) для изменения энтропии, мы можем представить принципиально не преобразуемую в работу за цикл теплоту выражением

dQ_х = Т_х (dQ_н / Т_н) = Т_х (dQ_рт / Т_рт ) = Т_хdS ,

из которого видно, что количество принципиально не преобразуемой в работу за цикл теплоты зависит от температуры холодильника тепловой машины и изменения в рабочем цикле энтропии рабочего тела, а именно равно их произведению. Здесь речь идет о том количестве энтропии, которое забирается рабочим телом у нагревателя и отдается холодильнику, и при этом понижается степень хаотичности состояния нагревателя, но в равной мере повышается степень хаотичности холодильника, а в целом хаотичность состояния всей системы остается неизменной. Поскольку каждый из сомножителей в правой части равенства в замкнутой системе не может быть равен нулю, то невозможно за цикл не отдавать часть теплоты холодильнику (утрачивая после этого возможность ее дальнейшего преобразования в работу).

Уравнение (5.1) показывает, что в теплоизолированной (δQ = 0) термодинамической системе энтропия может сохраняться, но это условие (отсутствие теплообмена с внешним миром) является лишь необходимым, но не достаточным для сохранения энтропии.

Опыт показывает, что в изолированных системах даже при отсутствии теплообмена энтропия может возрастать, если в них идут релаксационные процессы самопроизвольного выравнивания термодинамических параметров. Для возвращения системы в первоначальное состояние теперь необходимо внешнее воздействие – систему можно квазистатическим образом перевести в начальное состояние, используя отвод теплоты и вычисляя необходимое уменьшение энтропии согласно уравнению (5.1).

Спонтанные (самопроизвольные) изменения в адиабатически замкнутой (теплоизолированной) системе всегда ведут к возрастанию энтропии. В этой асимметрии течения природных процессов заключена причина различимости прошлого и будущего.

С течением релаксационных процессов в системе постепенно утрачивается возможность преобразования теплоты в работу, которая раньше существовала в силу наличия перепадов (неравномерности по объему) интенсивных параметров, например, при выравнивании температур нагревателя и холодильника у тепловой машины. Происходит также так называемая диссипация (рассеяние) энергии за счет работы сил трения, то есть превращение энергии макроскопических движений тел в энергию хаотического движения микрочастиц. Это означает, что самопроизвольно степень хаотичности состояния системы может только увеличиваться, но никогда не убывает, оставаясь неизменной в замкнутых системах лишь в случае протекания в них полностью обратимых процессов.

В необратимых процессах проявляется еще одно свойство энтропии, не связанное прямо с введением понятия энтропии, для чего было вполне достаточно рассмотрения полностью обратимых процессов (пусть даже в идеализированных экспериментах).

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ иногда формулируют как принцип неубывания энтропии при любых процессах, идущих в замкнутых системах, и записывают математически как (5.5)

Таким образом, второе начало термодинамики несет в себе двойное содержание.

Во-первых, принцип существования и сохранения энтропии, утверждающий существование функции состояния, характеризующей степень хаотичности состояния термодинамической системы, и сохранение этой функции в замкнутых системах, при условии протекания в них полностью обратимых процессов. Принцип сохранения энтропии означает невозможность никаким способом понизить энтропию в полностью изолированных термодинамических системах.

Во-вторых, принцип самопроизвольного возрастания энтропии в замкнутых системах при протекании в них необратимых процессов. Это значит, что степень хаотичности изолированной термодинамической системы, находящейся в неравновесном состоянии, самопроизвольно возрастает до тех пор, пока в системе не установится термодинамическое равновесие. При этом энтропия системы стремится к максимуму.

В тех случаях, когда энтропия возрастает не только за счет поступления в систему теплоты извне, но и за счет спонтанно (самопроизвольно) идущих релаксационных процессов, термодинамическое тождество превращается в неравенство Клаузиуса. В общей форме оно записывается в виде

TdS > dU + dA. (5.6)

Запишем его в форме, связанной с газообразным состоянием,

TdS > dU + PdV. (5.7)

Это неравенство играет большую роль при рассмотрении процессов приближения термодинамических систем к равновесию в случаях, когда система открыта, то есть, не изолирована от внешнего мира. Наше знание того, что при приближении системы к равновесию энтропия стремится к максимуму, позволяет через неравенство Клаузиуса найти функции (разные для разных случаев открытости), которые при приближении открытых систем к равновесию стремятся к своему экстремуму (минимуму). Этими функциями (аналогами потенциальной энергии для разных типов термодинамических процессов) являются: внутренняя энергия, энтальпия, свободная энергия и термодинамический потенциал Гиббса. Подробнее об этих функциях будет рассказано в следующей главе.

6. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

6.1. Максимальная работа в термодинамических процессах

Поскольку энергетические соотношения играют в термодинамике очень важную роль (вся термодинамика развивалась под влиянием практических потребностей преобразования теплоты в работу), то при расчетах особый интерес представляет аналог механической потенциальной энергии. Напомним, что в механике потенциальная энергия вводится как скалярная функция, позволяющая вычислить работу консервативной силы не через вычисление интеграла от элементарной работы вдоль всего пройденного пути, а просто как разность значений этой функции в начале и конце пути (что существенно упрощает вычисления). Нахождение работы силы является одной из важнейших задач механики. Однако в термодинамике, в отличие от привычной механики консервативных систем (где отсутствуют силы, зависящие от скоростей), система может переходить из одного состояния в другое, совершая разную работу, в зависимости от способа (пути) перехода, поскольку разное количество энергии передается частично силовым (работа), а частично тепловым (теплота) путем (хотя полное изменение внутренней энергии системы будет при этом тем же самым). Поэтому в термодинамике рассматривают четыре наиболее важных для практики процесса изменения состояния термодинамических систем. Так, например, изменение состояния системы без теплообмена с окружающей средой может происходить при неизменном объеме, а может - при постоянном давлении (с изменением объема). Роль потенциальной энергии в этих процессах будут играть разные функции, в первом случае – внутренняя энергия U, а во втором – так называемая энтальпия H (теплосодержание). Если процесс происходит при хорошем тепловом контакте, обеспечивающем постоянство и равенство температуры термодинамической системы с температурой внешней среды, то изменение состояния системы может опять происходить как при постоянном объеме, так и при постоянном давлении. Здесь в первом случае роль потенциальной энергии будет играть функция, называемая свободной энергией и обозначаемая обычно F, а во втором – термодинамическим потенциалом Гиббса (свободной энтальпией), который мы будем обозначать буквой G.

Таким образом, в термодинамике оказалось несколько аналогов потенциальной энергии в зависимости от вида процесса. Эти функции состояния термодинамической системы получили название термодинамических потенциалов. Изменения этих функций при переходе системы из одного состояния в другое позволяют вычислить максимальную работу, которую при этом система может совершить в самом благоприятном случае, когда нет потерь энергии. Еще раз напомним, что основной технической задачей термодинамики является создание максимально эффективных тепловых машин как источников механической энергии, то есть машин, преобразующих теплоту в работу.

6.2. Термодинамические потенциалы в адиабатных процессах

Термин адиабатный означает полную тепловую изоляцию системы. Самый простой случай при этом – обратимые процессы в полностью изолированных системах, то есть в системах, не имеющих никаких связей с внешним миром - ни тепловых, ни силовых, ни материальных (обмен веществом). В этом случае термодинамическое тождество (5.3) в силу равенства нулю левой части сразу показывает, что совершаемая системой работа против внешних сил может выполняться только за счет уменьшения ее внутренней энергии, то есть

dA_max = - (dU)_S,V (6.1)

Индекс max означает, что равенство выполняется только в идеальном процессе, происходящем без потерь энергии. Равенство (6.1) означает, что в полностью изолированных системах при сохранении энтропии и объема роль потенциальной энергии будет играть внутренняя энергия.

Если работа выполняется термодинамической системой в условиях теплоизоляции, но при наличии механических связей с окружающими телами, то такая работа выполняется не только за счет убыли внутренней энергии, но и за счет изменения потенциальной энергии системы как целого в поле внешних сил dE_пот. Основной случай механической связи – это связь, осуществляемая посредством внешнего давления (практически наиболее интересный случай), и тогда dE_пот = P_внешdV. Для элементарной работы газообразной системы при условии постоянного давления это дает

dA_max= - dU - dE_пот= - dU - PdV = - d(U+PV) = - (dH)_S,Р (6.2)

Уравнение (6.2) показывает, что роль потенциальной энергии для внешних сил (при постоянном давлении) у газа играет произведение давления на объем PV. Сумма внутренней энергии и этого произведения, играющая роль полной потенциальной энергии в изобарных процессах без теплообмена, получившая название энтальпия (теплосодержание) и обозначаемая обычно символом H,

H = U + PV, (6.3)

является термодинамическим потенциалом для адиабатных процессов при наличии силовой связи с внешним миром. Максимальная работа, которую может совершить термодинамическая система в таких условиях, равна убыли энтальпии. В присутствии электромагнитных влияний выражение для энтальпии принимает вид

H = U + PV – (D·E)/2 – (H·B)/2. (6.3’)

Стоящие в скобках скалярные произведения учитывают потенциальную энергию поляризованности и намагниченности вещества (в расчете на один моль) во внешних электрических (напряженность E)и магнитных (магнитная индукция B) полях. ЗдесьDиH – векторы электрического смещения и напряженности магнитного поля.

6.3. Термодинамические потенциалы в изотермических процессах

Очень важным для практических приложений является рассмотрение процессов, при осуществлении которых температура в системе успевает по всему объему выравниваться с температурой окружающей среды. Это означает, что теплота быстро поступает в систему из окружающей среды (или отводится). При постоянстве температуры термодинамическое тождество (5.3) можно переписать в виде

dAmax = - dU + TdS = - d(U – TS) = - (dF)Т,V, (6.4)

где через F обозначена свободная энергия, играющая роль потенциальной энергии для изотермических процессов в условиях постоянства объема термодинамической системы

F = U – TS. (6.5)

Совершенно аналогичным образом вводится термодинамический потенциал Гиббса (именуемый также свободной энтальпией). Он играет роль потенциальной энергии для изотермических процессов, идущих в системах, которые имеют хороший тепловой контакт с внешним миром и силовую связь с ним (постоянство температуры и давления).

Для газообразных систем при постоянном давлении

dAmax= - d(F+ PV) = - dU +TdS– PdV = - d(U–ТS+ PV) = - (dG) Т,Р, (6.6)

то есть потенциал Гиббса для газа

G = U – TS+ PV. (6.7)

В присутствии электромагнитных влияний этот потенциал записывается так

G = U – TS + PV - (D·E)/2 - (H·B)/2. (6.7’)

7. ТЕРМОДИНАМИЧЕСКИЕ УРАВНЕНИЯ СОСТОЯНИЯ

7.1. Отличие рассмотрения задач в механике и в термодинамике

Прежде всего, отметим качественное отличие описания процессов в механике и термодинамике. В механике есть уравнение движения (2-й закон Ньютона), а в термодинамике («термостатике») – термическое уравнение состояния (1.1), связывающее термодинамические параметры, знание которых для феноменологической термодинамики означает знание состояния термодинамической системы. Поскольку связь между параметрами (1.1) (существующая только в равновесных или близких к таковым состояниях) позволяет любой из параметров выразить через остальные, то описание процессов в термодинамике оказывается многовариантным. С примером этого мы уже встретились при описании адиабатного процесса в идеальном газе, где адиабатный процесс равносильно описывался тремя разными уравнениями (3.8), (3.9) и (3.10).

Возможность разных вариантов описания одного и того же термодинамического процесса породила в термодинамике проблему, которой нет в механике, а именно, проблему выбора переменных, выбора функций, наиболее удобно (с точки зрения практических приложений) описывающих процесс изменения состояния.

В 1875 году американский физик Гиббс показал, что для решения технических задач термодинамики вполне достаточно знать поведение в термодинамических процессах всего четырех функций, играющих в термодинамике роль, аналогичную роли потенциальной энергии в механике. Эти четыре функции соотносятся с четырьмя рассмотренными ранее процессами (два адиабатных и два изотермических), которых достаточно, чтобы смоделировать работу любого технически интересного термодинамического устройства. Термодинамических потенциалов четыре, так как в термодинамике четыре основные переменные – две механические для работы (давление и объем, то есть сила и перемещение) и две тепловые для теплоты (температура и энтропия), которые могут рассматриваться в качестве независимых координат термодинамических процессов. Это хорошо видно из выражений, описывающих два механизма передачи энергии термодинамической системе: dA = PdV и dQ = TdS.

Удерживая неизменными (закрепляя) по одной механической и одной тепловой координате, мы получаем четыре разновидности основных термодинамических процессов, которых достаточно, чтобы равновесным способом перевести термодинамическую систему из любого начального (равновесного) состояния в любое конечное (равновесное), и соответствующие им четыре термодинамических потенциала. А раз так, то необходимо научиться находить эти основные термодинамические потенциалы (точнее – разность их значений) в разных состояниях, то есть надо найти дифференциальные уравнения, связывающие скорость изменения термодинамических потенциалов со значениями термодинамических параметров и их производными (то есть с величинами, которые могут быть определены опытным путем). Эти уравнения получили название термодинамические уравнения состояния (в отличие от обычных, термических уравнений состояния, в которые входят только термодинамические параметры и которые либо очень сложны, либо вовсе нам неизвестны). Все эти уравнения выводятся из термодинамического тождества (5.3) (термодинамической формы записи закона сохранения энергии, учитывающей существование энтропии) ТdS = dU + dA.