Термодинамические уравнения состояния

Начнем с внутренней энергии, которую в термодинамическом тождестве можно представить через полный дифференциал двух переменных - температуры и объема, тогда

Дифференциал энтропии как функции двух переменных (Т,V) можно записать в виде

Сравнивая эти два выражения, находим, что

Поскольку вторые, перекрестные производные от функции двух переменных должны быть равны независимо от порядка дифференцирования, то есть

то, следовательно,

откуда

и мы имеем термодинамическое уравнение состояния для внутренней энергии (как функции объема при постоянной температуре).

Все величины, стоящие в правой части уравнения (7.1), легко поддаются измерению на опыте, что позволяет найти зависимость внутренней энергии от объема при разных температурах.

Знание этой зависимости позволяет найти разность теплоемкостей при постоянном давлении и постоянном объеме по уравнению (2.6), то есть технически важную характеристику термодинамических объектов.

Если переменными являются другие параметры, то термодинамическое уравнение состояния для внутренней энергии может быть записано просто по аналогии. Например, из уравнения (7.1) можно получить зависимость внутренней энергии аккумулятора от его заряда при разных температурах. Поскольку работа, совершаемая аккумулятором при перемещении по электрической цепи заряда q, равна произведению электродвижущей силы источника тока E(ЭДС) на величину заряда, то элементарная работа имеет вид dA = Edq. Сравнивая работу газа и работу источника тока, то есть dA = PdV и dA = Edq, мы видим, что здесь заряд играет роль объема, а ЭДС источника – роль давления. Теперь по аналогии с уравнением (7.1) можно получить зависимость внутренней энергии аккумулятора от его заряда через температурную зависимость ЭДС
аккумулятора

Поскольку температурная зависимость ЭДС при постоянном заряде легко находится опытным путем, то это уравнение приобретает прямую практическую значимость.

Термодинамическое тождество позволяет также получить уравнение, связывающее изменение энтальпии с термодинамическими параметрами. Поскольку H = U + PV, и значит dU = dH - PdV - VdP, а дифференциал энтальпии как функции температуры Т и давления Р имеет вид

то термодинамическое тождество (5.4) после замены dU и dH дает

В то же время дифференциал энтропии как функции температуры Т и давления Р

и, следовательно,

Из равенства перекрестных производных

получаем

откуда, после раскрытия скобок, окончательно имеем

Это - термодинамическое уравнение состояния для энтальпии (как функции давления при постоянной температуре), где правая часть легко определяется опытным путем.

Что касается термодинамических уравнений состояния для двух других термодинамических потенциалов, то есть свободной энергии F и термодинамического потенциала Гиббса G, то они находятся легче и выглядят проще, чем для внутренней энергии и энтальпии. Из уравнения (6.5), которое дает dU = dF + TdS + SdT, и термодинамического тождества TdS = dU + PdV получаем dF = - PdV – SdT.

С другой стороны, дифференциал свободной энергии как функции объема и температуры

Сравнивая эти два уравнения, находим скорость изменения свободной энергии в изотермическом процессе при изменении объема

Это термодинамическое уравнение для свободной энергии означает, что если мы знаем давление при некоторой температуре, то мы знаем быстроту изменения свободной энергии с изменением объема и можем вычислить ее изменение в изотермическом процессе.

Совершенно аналогичным образом находится выражение для дифференциала термодинамического потенциала Гиббса

Отсюда скорость изменения термодинамического потенциала в изотермическом процессе при изменении давления просто равна объему (это еще одно термодинамическое уравнение состояния)

Поскольку объем легко измеряется, то уравнение (7.4) позволяет вычислить изменение термодинамического потенциала Гиббса в изотермическом процессе при изменении давления.

Практический интерес в термодинамике представляют не абсолютные значения термодинамических функций, а их изменения при переходе системы из одного состояния в другое. Поэтому функции находят с точностью до произвольного постоянного слагаемого (и в этом смысле они похожи на потенциальную энергию в механике, которая отсчитывается от произвольного уровня, условно принимаемого за нулевой).

7.3. Система связей между термодинамическими функциями. Уравнения Гиббса - Гельмгольца. Соотношения Максвелла

Термодинамическое тождество (5.4) TdS = dU + PdV и определения термодинамических потенциалов H = U + PV (6.3), F = U – TS (6.5) и (6.7) G = U – TS+ PV позволяют записать полные дифференциалы энтальпии, свободной энергии и потенциала Гиббса в виде: dH = TdS + VdP, dF = - SdT – PdV, dG = - SdT + VdP. Отсюда сразу следуют связи

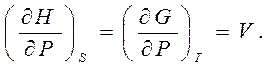(7.7)

Если подставить выражения для энтропии из (7.6) в уравнения (6.5) и (6.7) и учесть (6.3), то получатся уравнения Гиббса-Гельмгольца, связывающие термодинамические потенциалы друг с другом и с их производными по термодинамическим параметрам

Из выражений для полных дифференциалов свободной энергии и потенциала Гиббса (dF = - SdT – PdV и dG = -SdT + VdP) и по свойству равенства перекрестных производных

получаем соотношения Максвелла

Слева в этих уравнениях стоят скорости изменения энтропии в изотермических процессах при изменении объема или давления, а правые части этих уравнений легко находят опытным путем.

Вторые производные от потенциалов связывают важные для практики значения теплоемкостей при постоянном объеме или давлении с изменением энтропии

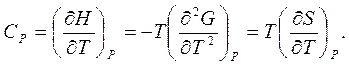(7.13)

Оба эти уравнения (7.13) имеют отношение к третьему началу термодинамики (теореме Нернста): При приближении температуры к абсолютному нулю энтропия однородной системы стремится к нулю, LimS]T=0 = 0. Строго говоря, энтропия обязана стремиться к постоянному значению, которое Макс Планк предложил для определённости всегда считать равным нулю.

В рамках феноменологической термодинамики третье начало термодинамики фиксирует точку отсчета энтропии. Энтропия при этом может быть вычислена по формуле

из которой видно, что вблизи абсолютного нуля теплоемкость должна становиться бесконечно малой (чтобы интеграл не обращался в бесконечность). Значит, никакими способами нельзя отнять теплоту у термодинамической системы, и абсолютный нуль недостижим.

Вторые производные от термодинамических потенциалов связаны также с коэффициентами сжимаемости - изотермическим kT и адиабатным kS - при соответствующих процессах (или с обратными им величинами – модулями всестороннего изотермического ВТ и адиабатного ВS сжатия). Произведения этих коэффициентов на объем дают вторые производные по давлению от термодинамического потенциала Гиббса G и энтальпии Н

а обратные им величины дают вторые производные по объему от

свободной энергии F и от внутренней энергии U

Для изохорного термического коэффициента давления b его произведение на давление (Рb) дает перекрестную производную от свободной энергии по температуре и объему со знаком минус (сравните с уравнениями 7.12) , так как в первом уравнении справа от знака равенства стоит произведение давления Р на изохорный коэффициент температурного давления β, а в правом уравнении – произведение объема V на изобарный коэффициент теплового расширения α со знаком минус

Вся эта система связей между термодинамическими функциями позволяет, зная любой из термодинамических потенциалов, найти все остальные. На практике снимают доступные экспериментальным измерениям зависимости и по ним строят графики или составляют таблицы зависимостей термодинамических потенциалов и энтропии от термодинамических параметров для самых различных веществ, а потом подбирают наиболее подходящие вещества в качестве самых эффективных рабочих тел в термодинамических процессах. Но это уже чисто технические задачи.

8. РЕАЛЬНЫЕ ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ

И ФАЗОВЫЕ ПРЕВРАЩЕНИЯ

8.1. Модель газа Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса

Модель идеального газа сыграла важную роль в исследованиях тепловых процессов. Она позволила выявить существование и зависимость от температур нагревателя и холодильника максимального КПД тепловых машин, позволила построить термодинамическую шкалу температур и, наконец, позволила понять второе начало термодинамики и ввести меру хаотичности состояния термодинамической системы – энтропию. Кроме всего этого, в силу предельной простоты термического уравнения состояния идеального газа, использование этого уравнения позволило найти фундаментальные, то есть обладающие всеобщностью, универсальностью, связи между термодинамическими потенциалами, термодинамическими параметрами и энтропией. Эти связи позволяют находить практически полезные характеристики термодинамических объектов даже в тех случаях, когда мы ничего не знаем об их термических уравнениях состояния (и даже вне зависимости от их агрегатных состояний, хотя сам идеальный газ имеет только одно агрегатное состояние – газообразное). Таким образом, идеальный газ оказался способным моделировать тепловое поведение в термодинамических процессах не только газообразных, но и жидких и твердых тел.

Однако целый ряд свойств реальных природных тел и процессов модель идеального газа заведомо не в состоянии объяснить в силу исключения из этой модели некоторых характеристик микрообъектов, составляющих термодинамическую систему. Так, например, модель идеального газа не может объяснить переход вещества из газообразного состояния в жидкое, поскольку за это ответственны силы взаимодействия между молекулами на расстоянии, которыми в этой модели пренебрегают. Эти силы получили название сил Ван-дер-Ваальса, но мы не будем подробно останавливаться на их природе, отметив только сам факт их существования.

Напомним, что в модели идеального газа пренебрегают размерами молекул, считая их материальными точками, а также их взаимным притяжением, которым действительно можно пренебречь, когда средние расстояния между молекулами измеряются десятками их радиусов и более. В этих случаях кинетическая энергия молекул газа много больше их потенциальной энергии взаимодействия на расстоянии, и этой потенциальной энергией можно пренебречь. Таким образом, модель идеального газа (как и любая модель) имеет свои границы применимости.

Если рассматривать явления природы, в которых собственные размеры молекул и их взаимодействие на расстоянии играют существенную роль (как, например, при фазовом переходе вещества из газообразного состояния в жидкое), то, естественно, такие явления не могут быть описаны с помощью уравнения состояния идеального газа. Следовательно, необходимо использовать другие модели, больше отвечающие реальности. Законы взаимодействия между молекулами можно постараться учесть, однако при этом все время надо помнить, что эти законы отличаются у разных веществ, и, следовательно, учитывающая их модель не будет обладать такой универсальностью как модель идеального газа.

Следующей по простоте моделью (после модели идеального газа) является модель газа, предложенная голландским физиком Ван-дер-Ваальсом. В ней учитывается как наличие собственного объема молекул, так и добавочное давление в газе, вызванное взаимным притяжением молекул. Отдельные молекулы, находящиеся в приграничном слое вещества, испытывают направленное внутрь силовое действие, которое можно считать пропорциональным концентрации молекул, а число молекул также пропорционально концентрации, и, следовательно, добавочное давление пропорционально квадрату концентрации (N/V)² молекул газа. А если еще из номинального объема газа вычесть собственный объем молекул, чтобы учитывать только свободный для движения молекул объем, то вместо уравнения идеального газа получается уравнение состояния для газа Ван-дер-Ваальса,

где a1 и b1 - две подгоночные константы, отнесенные к одной молекуле. В расчёте на один моль эти постоянные Ван-дер-Ваальса (не универсальные, а разные у разных веществ) суть а = NA²a1 и b = NAb1.

Теперь уравнение Ван-дер-Ваальса (в расчете на один моль) принимает вид

(P + a/V²)(V – b) = RT. (8.1)

Это уравнение качественно правильно отражает поведение реальных газов, хотя в количественном отношении полного совпадения нет.

Молярные постоянные Ван-дер-Ваальса а и b для всех веществ измерены и занесены в соответствующие таблицы.

Если нарисовать изотермы газа Ван-дер-Ваальса в координатах давление-объем, то они имеют вид, представленный на Рис. 4.

Р

Р_К К

Пар

С

Т_К

Д

в

V_А V_К V_Д V

Рис. 4. Изотермы газа Ван-дер-Ваальса

Как видно из рис.4, ниже некоторой (критической) температуры Т_к изотермы дают S-образный участок кривой АВСД, который в опытах с реальными газами не наблюдается. Вместо него между точками А и Д сосуществуют две фазы – жидкая и газообразная. Здесь газ частично конденсируется в жидкость так, что при изменении объема давление все время остается постоянным между точками А и Д, изменяется лишь доля молекул газа, находящегося в состоянии насыщенного пара, а изотерма представляет собой горизонтальную прямую. При температурах, заметно превышающих критическую температуру, изотермы Ван-дер-Ваальса не отличаются существенно от гиперболических изотерм идеального газа (Рис.1).

Точка К на критической изотерме представляет собой точку перегиба кривой. Как известно из математики, в точке перегиба не только первая, но и вторая производная обращается в нуль. Это позволяет в данной точке связать с постоянными Ван-дер-Ваальса значения давления Р_к, объема V_к и температуры Т_к, которые получили название критических. Они определяются из уравнений

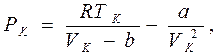
Сравнивая второе и третье уравнения, получаем

V_K = 3b, (8.2) а подстановка V_K во второе уравнение дает

Т_К = 8а/27Rb, (8.3)

и подстановка V_K и Т_К в первое уравнение дает

P_K = a/27b². (8.4)

Знание координат критической точки (V_K, P_K, Т_К), найденное опытным путем, позволяет выразить через них газовую постоянную R и обе константы Ван-дер-Ваальса по формулам

R = 8P_KV_K/3Т_К, b = V_K/3, a = 3P_KV_K² (8.5)

8.2. Фазовые переходы, их теплота и температура.