Холодильник и тепловой насос

В качестве рабочего тела тепловой машины Карно использовал идеальный газ, помещенный под поршень в сосуд с идеально теплопроводными стенками и совершающий полный (замкнутый) цикл, который подразделяется на четыре следующих этапа:

1. Изотермическое расширение, связанное с поглощением теплоты через хороший тепловой контакт с нагревателем, при одновременном совершении некоторой работы.

2. Адиабатное расширение (при отключении всех тепловых контактов рабочего тела, то есть при его полной теплоизоляции) с совершением еще некоторой работы и одновременным понижением температуры рабочего тела до температуры теплового резервуара, именуемого холодильником.

3. Изотермическое сжатие, требующее затраты работы внешних сил, при одновременном отводе теплоты от рабочего тела через идеальный тепловой контакт с холодильником.

4. Адиабатное сжатие (при ликвидации теплового контакта), вызывающее повышение температуры рабочего тела до температуры нагревателя, но требующее для своего осуществления еще некоторой работы внешних сил.

Этот цикл принципиально верно отражает работу любого теплового двигателя, так как рабочее тело обязательно должно получать откуда-то теплоту для процесса своего расширения с совершением положительной работы, а также необходим отвод теплоты для сжатия рабочего тела с совершением меньшей отрицательной работы. В противном случае не удается вернуться в исходное состояние с перевесом полученной работы над затраченной.

Все этапы цикла Карно предполагаются полностью обратимыми. Для этого они должны выполняться квазистатически. Используя в качестве рабочего тела идеальный газ, можно легко (уравнение состояния идеального газа простое) вычислить КПД этого цикла.

Если окажется, что КПД не зависит ни от типа процессов цикла, ни от вида рабочего тела (то есть в конечном результате не проявятся ни особенности процессов, ни специфика уравнения состояния), то это будет означать, что полученные при исследовании КПД этого цикла результаты являются универсальными.

Для лучшего понимания расчетов изобразим цикл Карно в координатах давление – объем (P,V). На Рис.3 цикл Карно представлен двумя отрезками изотерм (1-2) и (3-4) и двумя отрезками адиабат (2-3) и (4-1).

1

Р

Т₁ 2 Т₂ 4 T₂ 3

V₁ V₃ V₂ V₄

Рис.3. Цикл Карно в координатах давление-объем (Р,V).

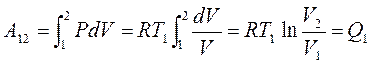На участке (1-2) газ изотермически расширяется, сохраняя температуру за счет притока тепла от нагревателя. Так как внутренняя энергия идеального газа на этом этапе не изменяется (она зависит от температуры и не зависит от объема), то вся полученная от нагревателя теплота расходуется на работу, совершаемую расширяющимся газом, и значит Q₁ = A₁₂.

Здесь использовано уравнение состояния идеального газа: PV = RT.

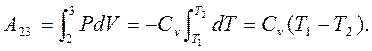На участке (2-3) в адиабатном процессе теплота не поступает, и газ совершает работу за счет своей внутренней энергии, в результате чего температура понижается до Т₂. Работа на этом участке

Здесь использовано уравнение (3.7) и постоянство теплоемкости C_v .

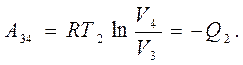Работа, совершаемая газом на участке (3-4) в изотермическом процессе при температуре Т₂ с отводом теплоты Q₂ в холодильник, вычисляется аналогично работе А₁₂ , то есть

Знак минус означает отвод теплоты от газа при его сжатии внешними силами, и работа газа при этом считается отрицательной.

Работа, совершаемая газом на участке (4-1) при его адиабатном сжатии вычисляется аналогично вычислению работы на участке (2-3)

А₄₁ = C_v(T₂ – T₁) = - A₂₃ .

и, следовательно, коэффициент полезного действия цикла Карно как отношение полной работы газа за цикл (положительной при расширении и отрицательной при сжатии),

А = A₁₂ + A₂₃ + A₃₄ +A₄₁, к полученной от нагревателя теплоте Q₁, равен

h = А/Q₁ = (A₁₂ + A₂₃ + A₃₄ +A₄₁)/Q₁ =

= [Q₁+C_v(T₁-T₂) – Q₂+ C_v(T₂ – T₁)]/Q₁= (Q₁ –Q₂)/Q_1.

Используя уравнение адиабаты идеального газа (3.8), можно записать процессы на участках (2-3) и (4-1) в виде:

T₁V₂^g-1 = T₂V₃^g-1 и T₂V₄^g-1 =T₁V₁^g-1.

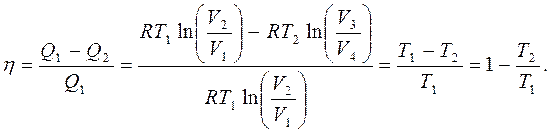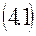Сопоставление этих уравнений показывет, что отношение объемов V₂/V₁ = V₃/V₄ одинаковое, и КПД цикла Карно

Итак, коэффициент полезного действия цикла Карно (две изотермы, две адиабаты и газ идеальный в качестве рабочего тела) оказался зависящим только от температур нагревателя и холодильника и ни от чего более. Для любых тепловых машин он является наибольшим из всех возможных, поскольку это КПД идеальной универсальной тепловой машины. Именно это свойство – полная обратимость цикла Карно – позволяет утверждать, что КПД цикла будет максимально возможным, так как никаких потерь энергии ни на одном этапе нет, а от типа использованных процессов КПД не зависит.

КПД цикла Карно тем больше, чем меньше отношение температур холодильника и нагревателя.

Очевидно, что любой встречающийся в технике цикл тепловой машины, представляемый замкнутой кривой на диаграмме давление-объем, то есть в координатах (P,V), можно с помощью мелкой сетки из адиабат и изотерм разделить на множество элементарных циклов Карно, а затем с помощью интегрирования вычислить результат. По этой причине нет оснований, рассматривать еще какие-либо циклы, так как любой цикл может быть смоделирован через цикл Карно.

Таким образом, действительно на преобразование теплоты в работу природой накладывается ограничение, имеющее принципиальный характер, и связанное с отношением температур холодильника и нагревателя. Обсуждению сущности этого ограничения, получившего наименование второго начала термодинамики, будет посвящен следующий раздел, а сейчас мы рассмотрим некоторые полезные для практики выводы из рассмотрения цикла Карно.

Цикл Карно является идеальным, то есть предельным по эффективности циклом относительно любой реальной тепловой машины. Отсутствие каких-либо потерь или нерационального расходования энергии на всех этапах связано с полной обратимостью всех рассматриваемых в машине Карно процессов.

Поэтому машину Карно можно заставить пройти все этапы цикла в обратном направлении, расходуя при этом внешнюю энергию в виде работы внешних сил и отнимая теплоту у более холодного резервуара и передавая ее более нагретому. Именно этим занимается обычный холодильник, понижающий температуру в некотором выделенном объеме пространства. Эффективность работы машины, решающей такую задачу, оценивается холодильным коэффициентом, определяемым как отношение изъятой из холодильной камеры теплоты Q₂ к работе, затраченной на перенос этой теплоты в резервуар с более высокой температурой (в комнату):

k = Q₂/A= Q₂ /(Q₁-Q₂) = T₂/(T₁ - T₂) = (1- h)/h. (4.2)

Это выражение показывает, что холодильный коэффициент тем больше, чем меньший перепад температур надо преодолеть для транспортировки теплоты от более холодного тела к более нагретому (и чем меньший КПД имеет при этом собственно цикл Карно).

Второй пример использования тепловой машины, работающей в обратном машине Карно направлении, это так называемый тепловой насос, который подобно холодильнику забирает теплоту у более холодного тела и передает ее более нагретому. Отличие в том, что здесь эффективность работы оценивается не по количеству изъятой у более холодного тела теплоты, а по количеству переданной более теплому. Таким образом, производительность теплового насоса определяется как отношение полученной нагреваемым телом теплоты Q₁ от более холодного тела к затраченной на этот перенос работе:

k = Q₁/A = Q₁/( Q₁ - Q₂) = 1/h. (4.3)

Здесь, как и в случае холодильника, коэффициент, характеризующий эффективность работы, оказывается больше единицы, но противоречия с законом сохранения энергии, конечно, нет. Нет, поскольку речь идет не о преобразовании энергии одного вида в другой, а только лишь о транспортировке энергии одного и того же вида (энергии хаотического движения микрочастиц) с одного уровня температуры на другой. Работа лишь позволяет, взяв некоторое количество теплоты от более холодного тела, передать большее количество теплоты более нагретому телу, и ничто не мешает количеству транспортируемой энергии быть больше, чем работа, затраченная на эту транспортировку (не говоря уже о том, что саму работу без препятствий можно преобразовывать в теплоту). На практике тепловой насос может использоваться для так называемого “динамического отопления”, когда взятая из внешней морозной атмосферы теплота используется для обогрева теплых жилых помещений.

4.3. Термодинамическая шкала температур

Первоначально, как уже упоминалось, температурная шкала строилась по тепловому расширению тел с использованием двух опорных точек, например, по точкам замерзания и кипения воды при нормальном давлении, с приписыванием этому температурному интервалу определенного числа градусов. Так, Цельсий делил этот интервал на 100 частей, Реомюр - на 80, а Фаренгейт – на 180. Этим делением определялся размер (величина) градуса.

С помощью цикла Карно можно дать определение температуры, не зависящее от частных свойств веществ, применяемых для градуировок температурных шкал, и тем самым определить (произвольно) размер градуса, поскольку для любой обратимой тепловой машины справедливо полученное из рассмотрения цикла Карно соотношение (см. (4.1))

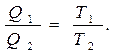(4.4)

Отношение температур двух тел определяется отношением теплоты, взятой рабочим телом у «горячего» тела, к теплоте, переданной «холодному» телу в обратимом процессе. Такие количества теплоты достаточно хорошо измеряются.

Из этого соотношения видно, что если холодильнику обратимой тепловой машины приписать определенную температуру (например, считать, что T₂ равно 1, или T₂ равно 200 или еще какому-либо числу), то температуру любого тела T₁ можно определить (считая ее равной температуре нагревателя в цикле Карно) по отношению теплот, передаваемых в обратимом циклическом процессе.

Определенная таким образом температура называется абсолютной термодинамической температурой. Это построение температурной шкалы было предложено Томсоном (лордом Кельвином).

Остается выбрать достаточно хорошо воспроизводимый термодинамический объект, (например, находящуюся в равновесии смесь льда, воды и пара, то есть воду в так называемой тройной точке, о чем смотрите параграф 8.3). Теперь надо приписать этому объекту некоторую определенную температуру (например, 273,16 градуса с той целью, чтобы размер градуса этой новой температурной шкалы был одинаковым с размером градуса в шкале Цельсия и чтобы 0^оС совпадал с точкой замерзания воды при нормальных условиях). Так была получена шкала температур Кельвина, которой мы впредь и будем, как правило, пользоваться.

5. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ

5.1. Формулировки второго начала и его суть.