Динамика плоско-параллельного движения тела.
Как было сказано в разделе кинематики плоско-параллельного движения тела достаточно рассмотреть движение плоской фигуры, задаваемым уравнением движения полюса и уравнением вращения фигуры

Задачей динамики плоско-параллельного движения тела является нахождение полученных уравнений по заданным силам (это основная задача динамики) или определение сил по заданному движению твёрдого тела. Часто встречаются смешанные задачи, когда между величинами, определяющими положение тела, имеются наперед известные соотношения, а действующие силы частью известны, частью должны быть определены по ходу решения задачи.
Теорема о движении центра инерции дает первое соотношение (3.78) при условии поступательного движения подвижной системы координат:
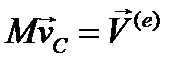
Это векторное равенство можно проектировать на те или иные оси. Проектируя его на оси неизменного направления х, у, получим два уравнения:
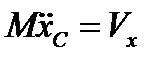 ,
, 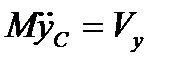 в которых
в которых 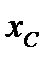 и
и 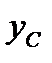 обозначают координаты центра инерции. Часто применяют также проектирование на касательную (
обозначают координаты центра инерции. Часто применяют также проектирование на касательную ( 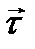 ) и главную нормаль (
) и главную нормаль ( 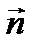 ) плоской траектории центра инерции :
) плоской траектории центра инерции :
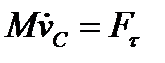 ,
, 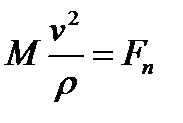 .
.
Здесь ρ- радиус кривизны траектории центра инерции. Дифференциальное уравнение вращения составим, применив теорему об изменении момента количества движения по отношению к центру инерции. В случае плоского движения твердого тела относительным движением по отношению к центру инерции является вращение тела с его угловой скоростью со вокруг оси, перпендикулярной к плоскости движения и проходящей через центр инерции С. Второе соотношение (101) даёт
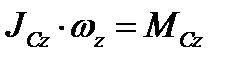
Таким образом, в декартовой системе координат уравнения плоскопараллельного движения будут
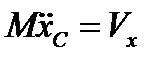 ,
, 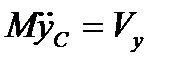
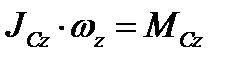
Если тело совершает несвободное движение, то в выражение главного вектора сил следует наряду с задаваемыми силами включить и реакции связей. Рассмотрим далее подробно часто встречающуюся задачу движения колеса по шероховатой плоскости. При качении цилиндра (колеса) контакт между колесом и поверхностью происходит не в точке, а из-за деформации колеса или самой поверхности реакция поверхности распределена на некотором участке. Так как рассматривается плоское движение, то и распределённую реакцию образует плоская система сил, которая может быть заменена равнодействующей. Рассмотрим два случая: движение под действием силы, приложенной в центре колеса и под действием крутящего момента.
| Q |
| mg |
| N |
| T |
| F |
| k |
| P |
| Рис. 57 |
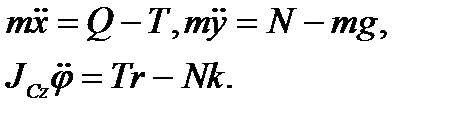 (3.79)
(3.79)
Индекс «С» в дальнейшем будем опускать, здесь r радиус колеса, k- коэффициент трения качения. Для определённости пусть момент инерции равен  . Так как колесо движется горизонтально, не подпрыгивая, то из второго уравнения следует
. Так как колесо движется горизонтально, не подпрыгивая, то из второго уравнения следует 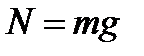 . Возможны два вида движения: без скольжения, тогда мгновенный центр скоростей находится в точке Р и со скольжением. Для первого случая можно записать условие
. Возможны два вида движения: без скольжения, тогда мгновенный центр скоростей находится в точке Р и со скольжением. Для первого случая можно записать условие 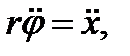 тогда, сложив первое и третье уравнения, получим
тогда, сложив первое и третье уравнения, получим
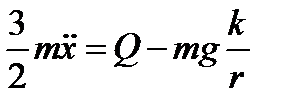
откуда имеем
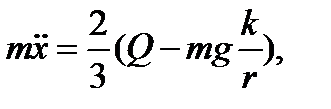
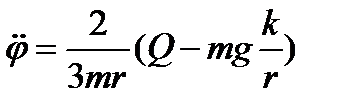 . (3.80)
. (3.80)
Определим из первого уравнения (3.79) силу Т, которую по смыслу можно назвать силой трения между колесом и поверхностью. Подставив (3.80) в первое уравнение (3.79) получим 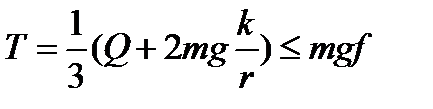 , при этом
, при этом 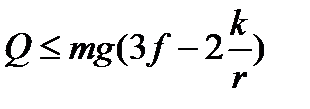 . Если сила Q больше, то уравнения движения запишутся так
. Если сила Q больше, то уравнения движения запишутся так
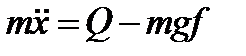
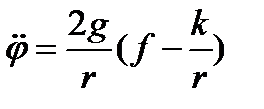
т.е. два независимых уравнения для 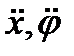 . В случае, если колесо не двигалось,
. В случае, если колесо не двигалось, 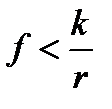 и
и 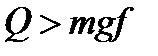 , то колесо будет скользить и не вращаться, т.е. двигаться поступательно.
, то колесо будет скользить и не вращаться, т.е. двигаться поступательно.
| М |
| mg |
| N |
| T |
| F |
| k |
| P |
| Рис. 58 |
Уравнения движения запишутся в виде
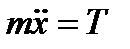 ,
, 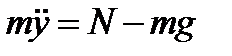 ,
, 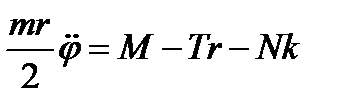 .
.
Пусть колесо движется без скольжения, тогда
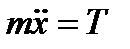 ,
, 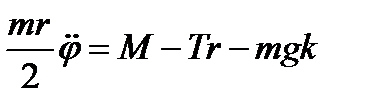
Как и в предыдущей задаче возможны два вида движения: без скольжения, тогда мгновенный центр скоростей находится в точке Р, и со скольжением. Для первого случая можно записать условие 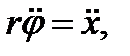 тогда, разделив третье уравнение на r и сложив первое и третье уравнения получим (при этом Т сократится)
тогда, разделив третье уравнение на r и сложив первое и третье уравнения получим (при этом Т сократится)
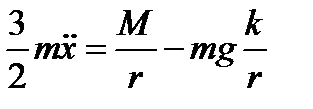
Сила Т, которую и здесь назовём силой трения, будет равна
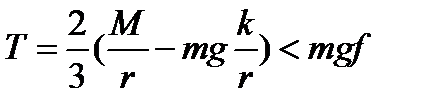
т.е. скольжение колеса будет происходить, если 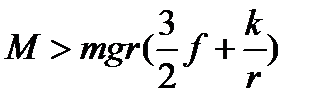 .
.
Если это условие выполняется, то получаем два независимых уравнения для движения центра колеса и его вращения
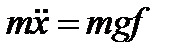 ,
, 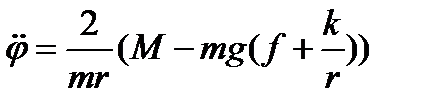 .
.
Дата добавления: 2019-12-09; просмотров: 569;











