Общий случай движения твердого тела.

Общий случай движения свободного твердого тела в пространстве всегда можно разбить на два более простых движения: поступательное движение вместе с произвольно выбранным полюсом и вращательное движение вокруг этого полюса. Такому представлению движения твердого тела соответствуют и уравнения движения, которые распадаются на уравнения движения полюса и урав­нения вращения твердого тела. Уравнения движения полюса получим, используя теорему об изменении количества движения системы 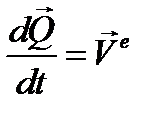, здесь 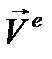— главный вектор внешних сил, приложенных к твёрдому телу, а количество движения твердого тела определяется формулой

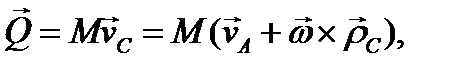(3.69)

где М - масса твердого тела; v_A, v_c — скорости полюса и центра инерции тела; 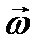—его угловая скорость, а 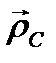—радиус-вектор, проведенный из полюса А в центр инерции тела С. Подстановка количества движения твердого тела (3.69) в теорему об изменении количества движения дает

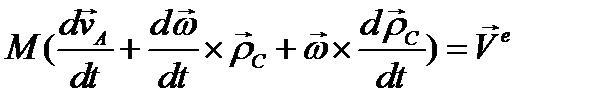(3.70)

Поскольку, как уже указывалось, удобнее составлять уравнения движения в осях, связанных с твердым телом, необходимо абсолютные производные, стоящие в соотношении (3.70), выразить через относительные по формуле (3.62); тогда

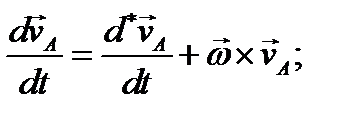
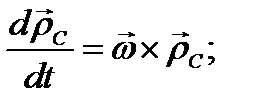
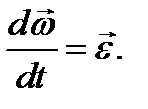(3.71)

Здесь уже принято во внимание, что 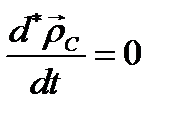, так как для наблюдателя, связанного с твердым телом, вектор 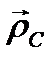постоянен. Подставив формулы (3.71) в уравнение (3.70), получим

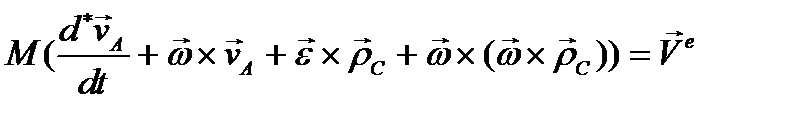(3.72)

Уравнение (3.72)- дифференциальное уравнение движения полюса А эквивалентно трем уравнениям в проекциях на оси х, у, z, связанные с телом; проектируя его, например, на ось х, имеем:

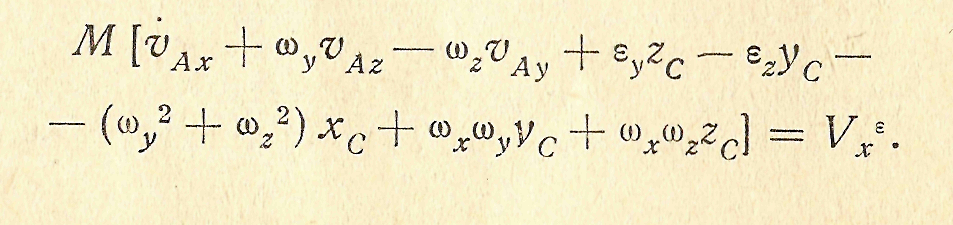(3.73)

Остальные два уравнения (в проекциях на оси у и z) по­лучаются из уравнения (3.73) круговой перестановкой индек­сов.

Переходим к выводу дифференциального уравнения вра­щения твердого тела вокруг полюса А. Для этого в теорему об изменении кинетического момента следует подставить общее выражение кинети­ческого момента (3.58), которое в данном случае вы­годнее представить так:

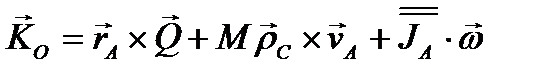(3.74)

Беря абсолютные производные по времени, находим

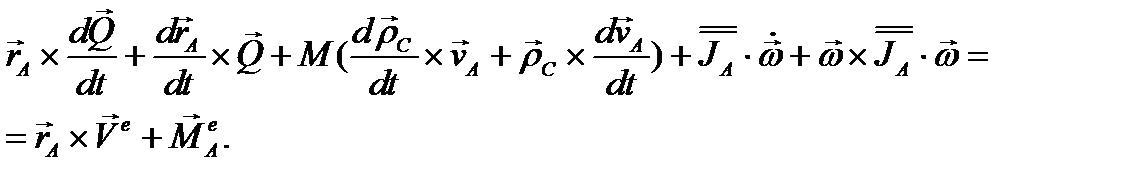(3.75)

В правой части уравнения (3.75) совершен известный пе­реход от главного момента относительно точки О к главному моменту относительно точки А (полюса); при этом первые слагаемые в левой и правой частях сокращаются. Учитывая далее формулы (3.69), (3.71), преобра­зуем уравнение (3.75) к следующему виду:

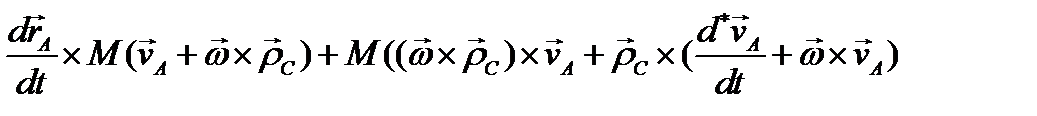
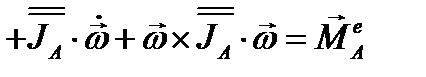
Но первое слагаемое в полученном соотношении тождественно равно нулю, а второе и третье - сокра­щаются, поэтому уравнение вращения твердого тела вокруг полюса А примет такой вид:

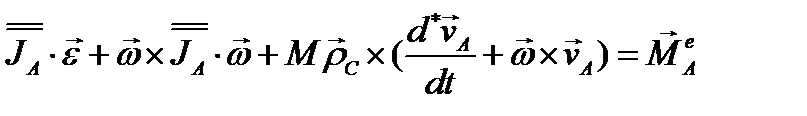(3.76)

Уравнение (3.76) эквивалентно трем уравнениям в проек­циях на оси х, у, z, связанные с твердым телом; проекция его на ось х будет выглядеть так (напоминаем, что оси х, у, z – главные оси инерции в точке А

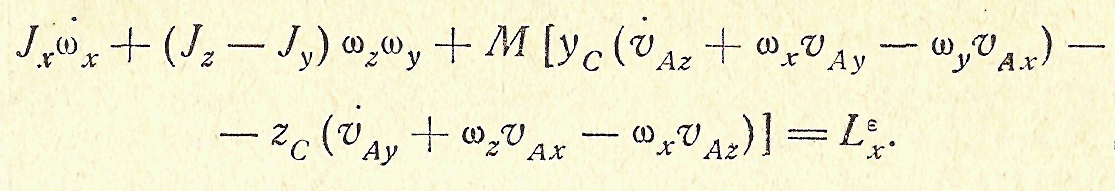(3.77)Остальные два уравнения (проекции на оси x и y ) можно получить из уравнения (3.77) круговой перестановкой индексов. Если полюс А поместить в центр инерции тела С, то 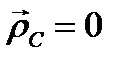и уравнения (3.72) и (3.76) существенно упрощаются; в этом случае имеем

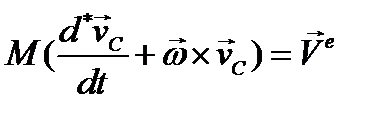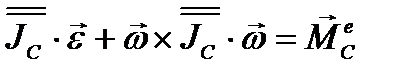; (3.78)

Именно эти уравнения обычно употребляются при изучении движения твёрдого тела в пространстве (самолёт, подводная лодка и т.д.).