Задача о физическом маятнике.

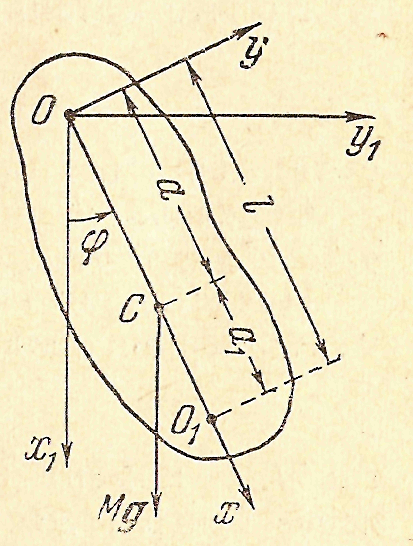
Как частный случай вращения тела вокруг неподвижной оси можно рассмотреть задачу о физическом маятнике. Физическим маятником называется твердое тело, вращаю­щееся вокруг неподвижной оси под действием силы тяжести. Рассмотрим случай, когда ось вращения горизонтальна. Проведем через центр тя­жести С тела плоскость, перпендикулярную к оси вращения. Точка пересечения О этой плоскости с осью вращения называется точкой подвеса. Примем эту точку за на­чало координат. Ось z направим по оси вращения, оси х и у расположим в пло­скости, проходящей через центр тяжести и точку подвеса, перпендикулярно к оси вращения (рис. 60 ). Дифференциальные уравнения вращения тела вокруг оси z ( если ось z главная) согласно предыдущего параграфа запишутся

Рис 60

следующим об­разом:

Так как в этом случае 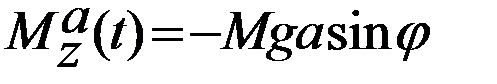, где М — масса тела, а — расстояние от точки до центра тяже­сти (а = ОС), то дифференциальное уравнение движения тела примет вид

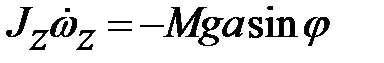
или

Рассмотрим случай малых колебаний, для которых можно принять . Тогда уравнение движения можно записать в следующей форме:

а его общее решение имеет вид

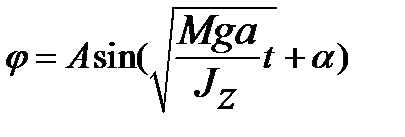
Отсюда следует, что угол φ изменяется по гармоническому за­кону с периодом колебаний, равным

Сравнивая дифференциальное уравнение движения матема­тического маятника с уравнением движения физического маятника, можно утвер­ждать, что математический маятник, имеющий длину

l= , (3.83)

будет двигаться так же, как и физический маятник. Величина l, определяемая формулой (3.83), называется приведенной длиной физического маятника. Представляя по формуле Гюйгенса мо­мент инерции тела относительно оси z в виде

где — радиус инерции тела относительно оси, проходящей через центр тяжести тела параллельно оси z, получим или

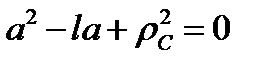
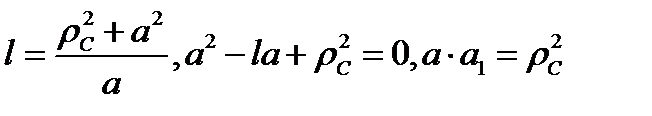
Полученное квадратное уравнение имеет два корня: и причём (по теореме Виетта) 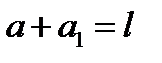и 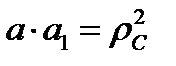. Откладывая l от точки подвеса в направлении центра тяжести, получим точку О1(см. рис 60), которая на­зывается центром качания. Таким образом, если старый центр качания сделать новой точкой подвеса, то старая точка подвеса станет новым центром качания. Способ качания с использованием теории физиче­ского маятника используется для экспериментального определения момента инерции неоднородных твердых тел или тел сложной конфигурации.

Вопросы для самопроверки.

1. Напишите дифференциальное уравнение вращения тела вокруг неподвижной оси (ось вращения главная).

2. Что такое статическая и динамическая уравновешенность тела, вращающегося вокруг неподвижной оси?

3. Напишите дифференциальные уравнения плоского движения тела.

4. Напишите уравнения кинетостатики. Прокомментируйте введённые обозначения.

5 Чему равна сила трения цилиндра, катящегося по шероховатой поверхности (разберите два случая).

6. Сколько степеней свободы имеет свободное тело, какими обобщенными координатами можно описать его движение?

L

Зад 9

L

2L

7. Чему равна приведённая длина однородного стержня длины l, колеблющегося вокруг горизонтальной оси (разберите разные случаи крепления оси: в конце стержня, на расстоянии 1/4l от конца стержня и т.д.)

8.Как изменится угловая скорость вращения стержня длины L и массы M1 , если груз массы М переместится из положения h на конец стержня.

9. Определите период колебаний двух стержней, показанных на рисунке, относительно горизонтальной оси.

R-радиус диска J-момент инерции диска

М

10. Напишите формулу Гюйгенса.

11. Как изменится центробежный момент инерции Jyz при переходе от старой оси OZ к новой, пересекающей ось 0Y на расстоянии l.

12. Определить ускорение груза и натяжение нити в указанном примере..

Глава 13.