Tермодинамика денатурации

Рассмотрим химическую реакцию денатурации белка, то есть переход молекул из нативного в денатурированное состояние N → D.

По состоянию равновесия считается такое состояние химической реакции, при котором соотношение количества молекул в нативном N и денатурированном D состояниях не меняется. Эта реакция может протекать как в прямом, так и в обратном направлении. К достижению состояния равновесия одно состояние преобладает над другим, а в состоянии равновесия устанавливаются такие скорости реакций, количества N и D не изменяются. Состояние химического равновесия зависит не от тех условий, в которых происходит реакция, а от тех, в которых поддерживается равновесие[125].

Как следует из общей теории [125], при постоянных температуре и давлении в состоянии равновесия термодинамический потенциал системы G минимален. Условие минимальности G можно записать в виде равенства к нулю полной производной по количеству частиц одного из реагентов:

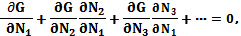(5.1)

где N_i - количество частиц различных веществ, участвующих в реакции. Изменения N_i во время реакции связаны друг с другом уравнением реакции:

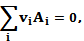(5.2)

Где А_i - химические символы веществ, реагирующих, а V_i - коэффициенты реакции (цели отрицательных чисел для выходных и положительные для конечных продуктов реакции),

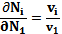(5.3)

С (5.1) и (5.3) следует:

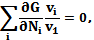(5.4)

или через химический потенциал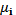

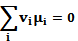(5.5)

Уравнение (5.5) представляет собой условие химического равновесия. Химический потенциал каждой из растворенных веществ получается дифференцированием термодинамического потенциала по числу частиц этого вещества:

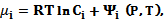(5.6)

где R - универсальная газовая постоянная, Т - абсолютная температура, Ci=Ni/N концентрация i-го вещества.

С условием химического равновесия (5.5)

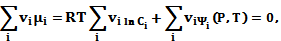(5.7)

вытекает закон действующих масс:

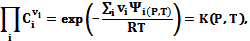(5.8)

где К {Р, Т) - константа химического равновесия.

Относительно рассматриваемого случая, в условиях термодинамического равновесия ∆G = 0, скорости прямой N → D и обратной N ← D реакции одинаковы, и соотношение между количеством исходного N и конечного D продуктов определяется константой химического равновесия К (Р, Т).

Определим изменение объема смеси веществ, реагирующих, в результате реакции, протекающей при постоянном давлении (и температуре) в слабых растворах. Для некоторого малого числа ∆n элементарных реакций:

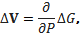(5.9)

где ∆G - соответствующее изменение термодинамического потенциала. Учитывая, что

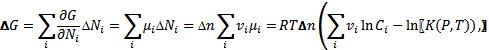(5.10)

получаем:

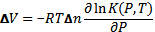(5.11)

Если реакция идет с увеличением ∆V> 0, то константа равновесия уменьшается с увеличением давления

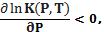
что означает сдвиг равновесия в сторону образования исходных веществ. и наоборот, реакции, которые протекают с уменьшением объема ∆V<0, ускоряются давлением 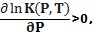что означает смещение равновесия в сторону образования продуктов реакции (имеющие меньший объем). Этот вывод согласуется с принципом Ле-Шателье, согласно которому реакция системы должна ослаблять внешнее воздействие. Например, незначительные изменения удельного объема в кристаллических структурах различной симметрии обусловливают существование различных фаз льда [126] при различных сочетаниях температуры и давления (см. Рис. 5.1).

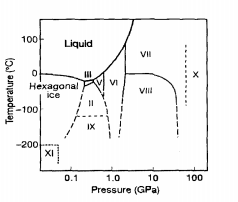
Рис. 5.1 – Фазовая диаграмма воды демонстрирует некоторые существования разных форм льда (по данным [126])

Кинетика денатурации

Внешние изменения температуры Т и/или давления Р выводят систему из термодинамического равновесия ∆G ≠ 0 и стимулируют реакцию в прямом N→D или обратном N ←D направлениях при ∆G < 0 или ∆G > 0 соответственно. Как показывает опыт, скорости этих реакций достаточно малы. Поэтому можно говорить о неполном термодинамическом равновесии системы - равновесие по отношению к движению молекул устанавливается значительно быстрее, чем равновесие по отношению к их взаимных превращений, то есть по отношению к составу N + D. Таким образом, можно рассматривать неполное равновесие системы как равновесие при заданном химическом составе [125, 127].

Анализ экспериментальных данных показывает, что денатурация белка N → D является процессом активационного типа, то есть проходит через образование некоторого неустойчивого промежуточного соединения под названием «Активированный комплекс» A*:

N→A*→D

Таким образом, на пути из своего исходного состояния до конечной системы должна преодолеть своего рода энергетический барьер. Энергия активации реакции примерно равна приросту средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что когда прямая реакция является экзотермической, то энергия активации обратной реакции U' выше, чем энергия активации прямой реакции U. Энергии активации прямой и обратной реакций связаны друг с другом через изменение внутренней энергии в ходе реакции. Выше сказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 5.2). Поскольку температура является мерой средней кинетической энергии частиц, повышение температуры приводит к увеличению количества частиц, энергия которых равна или больше энергии активации, что приводит к повышению константы скорости k.

Влияние температуры на скорость реакции задается эмпирической формулой Аррениуса [127]:

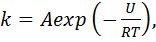(5.12)

где U - активационный барьер между реагентами и продуктом (в расчете на моль вещества). Достоверность этой формулы подтверждается теоретическими расчетами для различных упрощенных моделей. Следует вспомнить теории активных сталкивающихся, теорию активированного комплекса, расчеты поверхностей потенциальной энергии, броуновскую динамику в энергетическом пространстве на основе уравнения Фокера-Планка[125, 127,128]. Все эти теории ведут к формуле (5.12) для константы скорости химической реакции, отличаются только выражения для предэкспоненцийного множителя А. Так, согласно с [128], величину А можно примерно определить как

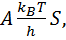(5.13)

где 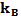- постоянная Больцмана, h - постоянная Планка, а фактор s (можно определить из статистической механики) принимает значения от 1 (атом-атомные реакции) до 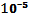(две нелинейные молекулы) [128]. При физиологической температуре Т = 310 К, величина отношения ( 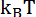)/h ≈ 6,5 • 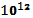Гц. Сравнение скоростей реакции при различных температурах дает оценку величины активационного барьера при нормальном давлении.

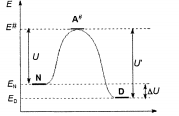
Координата реакции

Рис. 5.2 - Энергетическая диаграмма процесса денатурации белка. Здесь 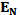- средняя энергия в нативном, а 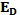- в денатурированном состоянии, U- активационный барьер денатурации, а U' - ренатурация, ∆U- изменение внутренней энергии при денатурации

Ниже (тема 10) приведены подробное обсуждение микропроцессов, сопровождающих денатурацию белков и природы активированного комплекса А*. Запишите явную параллель между баро- и термоденатурацией с точки зрения термодинамики.