Дифференциальные уравнения вращения твердого тела.

В кинематике была получена формула, связывающая абсолютную и относительную производные переменного вектора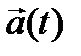

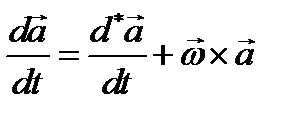(3.62)

Напомним, что здесь 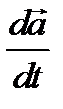- абсолютная производная, вы­деляемая неподвижным наблюдателем; 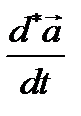- относительная производная, вычисляемая подвижным наблюдателем; 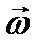- угловая скорость подвижного наблюдателя. Перейдем к составлению уравнений движения твер­дого тела, вращающегося вокруг неподвижной точки О. Кинетический момент твердого тела в этом случае вы­ражается формулой

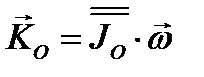
(Свяжем систему осей Oxyz с вращающимся телом и воспользуемся теоремой об изменении кинетического момента с учётом формулы (3.62)

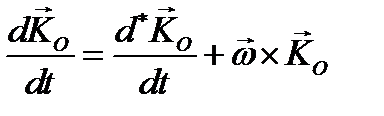(3.63)

Тензор инерции твердого тела в осях, связанных с самим телом, будет постоянным, поэтому относительная производная его будет 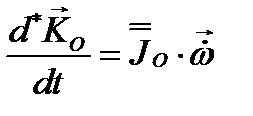, и выражение (3.63) следует записать в виде

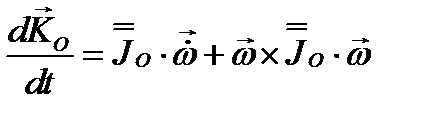
Тогда векторное уравнение вращения твердого тела вокруг не­подвижной точки будет иметь вид

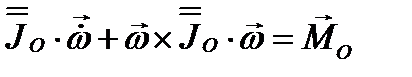(3.64)

Предполагая оси х, у, z главными, имеем

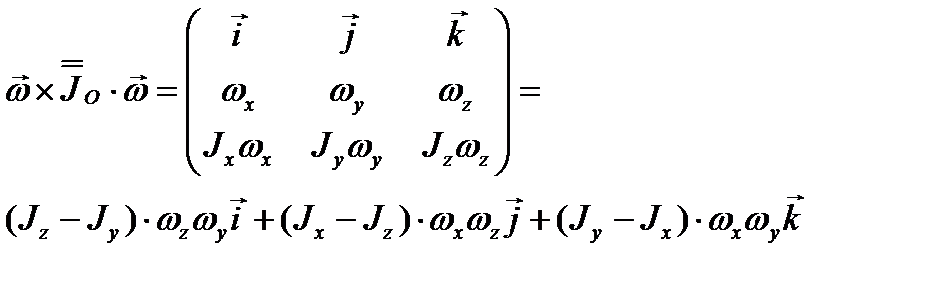
Проекции уравнения (3.64) на оси, связанные с телом, будут

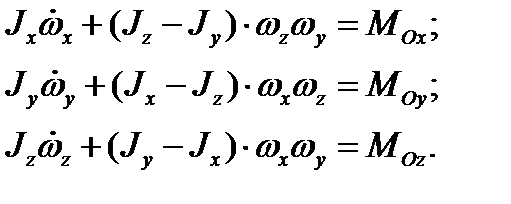(3.65)

Уравнения (3.65) называются динамическими уравнениями Эйлера.

Если удобнее рассматривать уравнения вращения в про­екциях на подвижные оси х', у', z', не связанные с твердым телом (а такие случаи бывают, например, в теории гироско­пов), то уравнение (3.65) следует предварительно преобразо­вать: 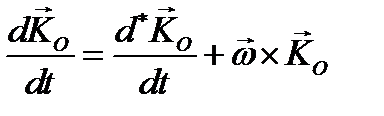, Здесь 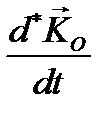- относительная производная кинетического мо­мента, вычисленная наблюдателем, связанным с системой осей х', у',z', а 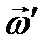- угловая скорость этой системы. Проектируя изменённое уравнение (3.65) на оси х', у',z' - получаем

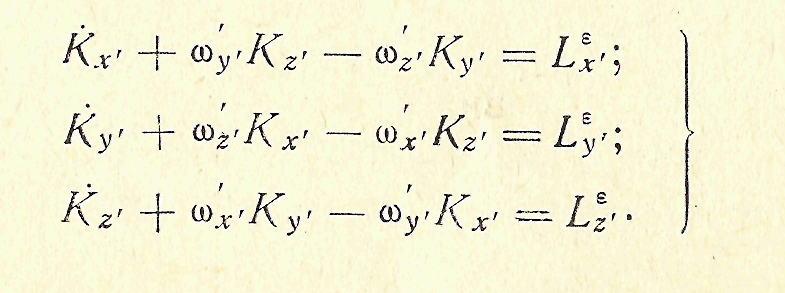
Полученные уравнения называют видоизмененными уравнениями Эйлера.

Пример. Рассмотрим вопрос об устойчивости вращения твердого тела по инерции. Пусть твердое тело, закрепленное в точке О, вращается вокруг одной из главных осей инерции (например, вокруг оси Ох), и движущие моменты полностью компенси­руют моменты сопротивлений, т. е. 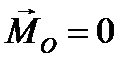. Тогда решение 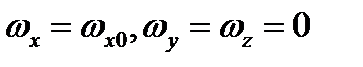удовлетворяет уравне­ниям Эйлера (3.65) с нулевыми правыми частями. Будет ли это решение устойчивым? Для выяснения этого вопроса исследуем возмущенное движение, угловые скорости которого представляются выра­жениями

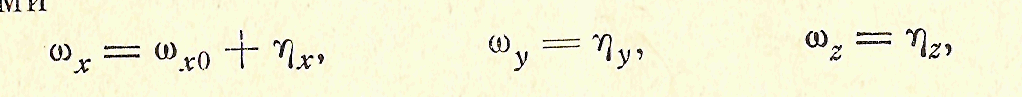(3.66)

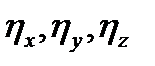- малые возмущения (малые функции времени). Подставляя величины (3.66) в уравнения Эйлера с нуле­выми правыми частями и отбрасывая величины второго по­рядка малости, получим

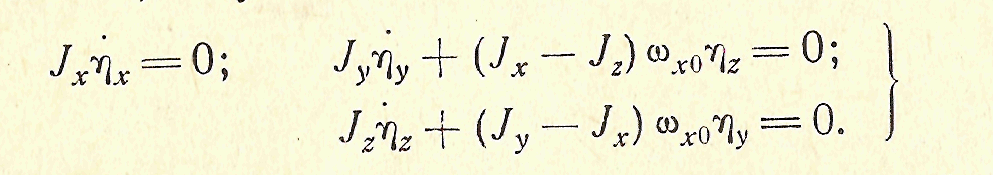(3.67)

Из первого уравнения (3.67) следует, что 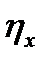= const; остав­шиеся неизвестные ( 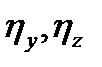) будут решениями уравнения

,

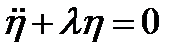где

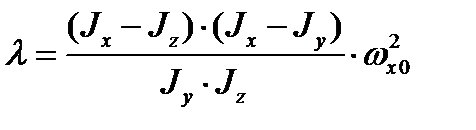(3.68)

Очевидно, что устойчивость невозмущенного движения бу­дет иметь место при ограниченных решениях уравнения (3.68), что, в свою очередь, будет при положительных значениях коэффициента 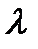. Тогда условие устойчивости нашего не­возмущенного движения переписывается так: 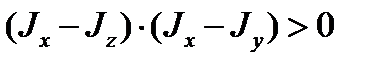, и оно будет выполнено при вращении по инерции вокруг главной оси с наибольшим или с наимень­шим моментом инерции.