Реакция оси вращающегося тела.

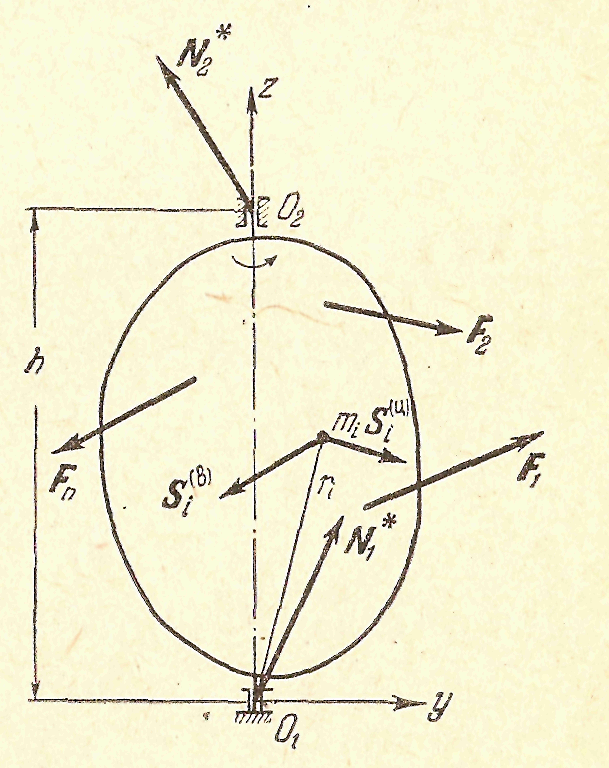
Рис 59

Рассмотрим ещё одну задачу на применение общих теорем динамики твёрдого тела: на вопросе об определении реакций в точках закрепления оси вращающегося твердого тела. Примем ось вращения за ось Oz, поместив начало системы осей 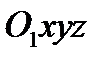, связанных с телом, в закрепленной точке 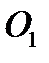(подпятник); в точке 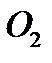на расстоянии 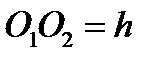помещен подшипник оси вра­щения (рис.59). 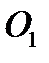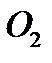Применим обе теоремы: освободив мысленно тело от опорных закреплений ,и введём в рассмот­рение искомые реакци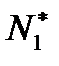и и 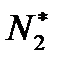. Запишем теорему о движении центра масс

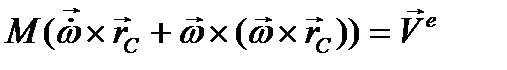
где 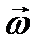- вектор угловой скорости тела, 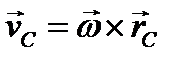- скорость центра инерции, 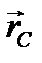- его вектор-радиус. Вычислим кинетический момент (по второй формуле (3.78)

.

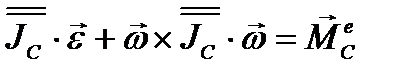Спроектируем полученные уравнения на оси координат 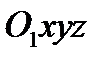жестко связанные

телом, заметим, что 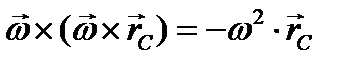. Тогда первая группа уравнений имеет вид

, , .

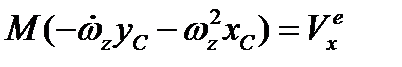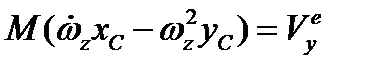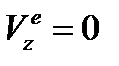Перейдём ко второй группе и рассмотрим сначала второе слагаемое

,

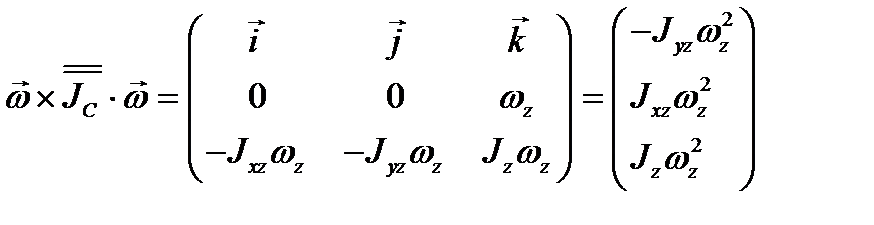после чего можем записать три уравнения

, ,

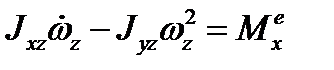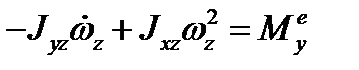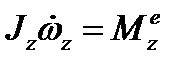
Рассматриваемую задачу можно решать и методом кинетостатики, для чего надо ввести силы инерции и моменты сил инерции ( на рисунке 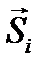и 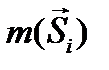). Будем считать, что тело вращается под действием крутящего момента 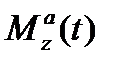, тогда проектируя 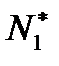и 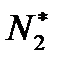на оси координат получаем шесть уравнений

,

,

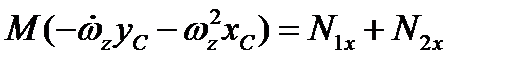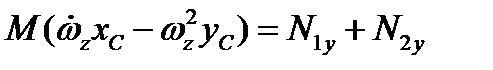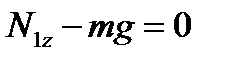, (3.81)

,

,

.

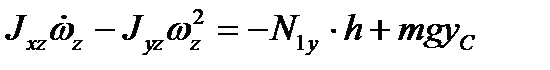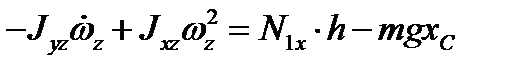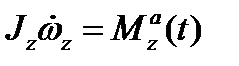Первые пять уравнений служат для определения пяти реакций 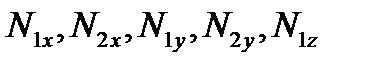, а последнее для определения угловой скорости. Рассмотрим некоторые частные случаи.

1. Если тело не вращается, то мы имеем 5 уравнений статики, из которых определяем 5 статических реакций.

2. Интегрируя последнее уравнение (3.81), получаем 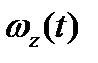. Тогда можно определить те динамические добавки к статическим реакциям, возникающие от вращения тела. Всегда можно выбрать оси таким образом, чтобы центр масс находился, к примеру, в плоскости Oyz, тогда 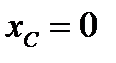и имеем

,

,

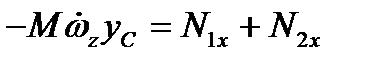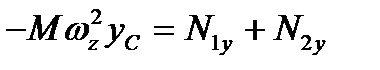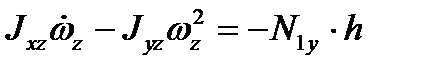, (3.82)

.

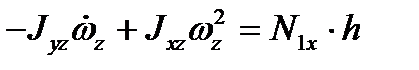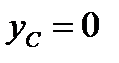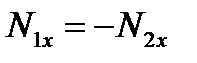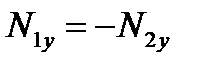3.Пусть ось вращения – центральная ось, тогда и , т.е. и или 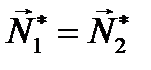. Дополнительное воздействие вращающегося тела на ось вращения приводится к паре сил и величина момента этой пары равна 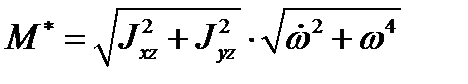. В этом случае говорят, что тело статически уравновешено.

4.Пусть ось вращения главная ось инерции в точке пересечения оси вращения и плоскости перпендикулярной оси вращения и проходящей через центр масс ( нецентральная ось не может быть главной во всех своих точках), тогда 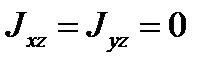и пусть расстояние от выбранной точки пересечения до подшипников равно а и в ( 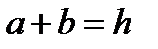). Тогда уравнения (109) следует переписать так

,

,

, .

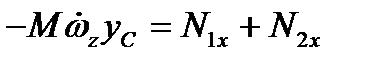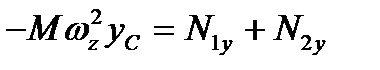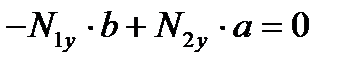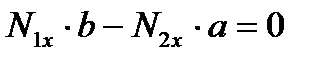Из последних двух формул следует 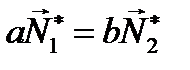и

, , , .

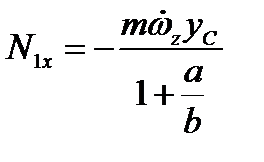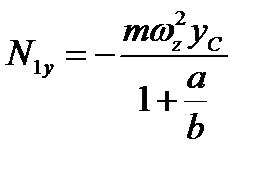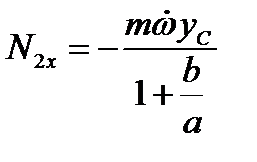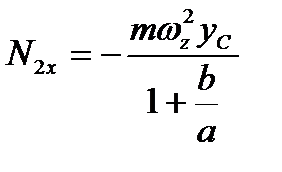Динамические реакции представляют параллельные силы, и в этом случае говорят, что тело динамически уравновешено.