Кинетический момент твердого тела.

Кинетический момент (главный момент количеств движе­ния) системы материальных точек относительно неподвиж­ной точки О определяется формулой

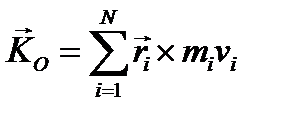(3.52)

Здесь векторы-радиусы 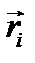проводятся из неподвижной точки О. Для твердого тела сумма в формуле (3.52) заменя­тся интегралом

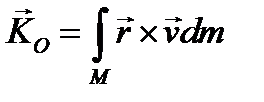(3.53)

где интегрирование производится по объему, занимаемому твердым телом. Пусть известна скорость некоторой точки А твердого тела (полюса) 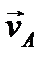, а также его угловая скорость 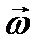; по известной формуле кинематики скорость любой точки твердого тела и ее вектор-радиус 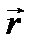выражаются формулами

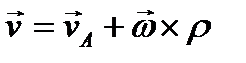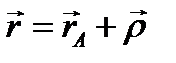; (3.54)

где 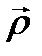- вектор-радиус, проведенный из полюса А в эту точку. Подставляя формулы (3.54) в кинетический момент (3.53), вынося векторы, не зависящие от положения текущей точки, за знак интеграла, получаем

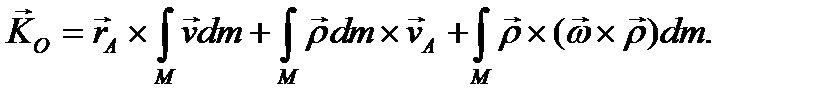(3.55)

Первые два интеграла в формуле (71) имеют простой смысл:

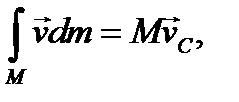
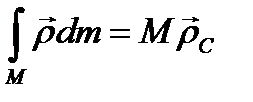(3.56)

для преобразования последнего интеграла (3.55) раскроем двойное векторное произведение, после чего используем свой­ство единичного тензора 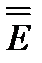и определение тензора инерции; тогда

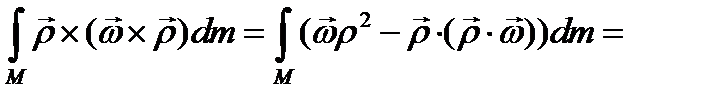
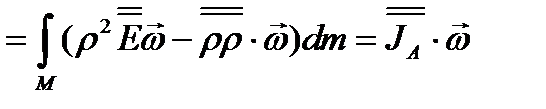(3.57)

Учитывая результаты (3.56) и (3.57), приводим выражение кинетического момента твердого тела к окончательному виду

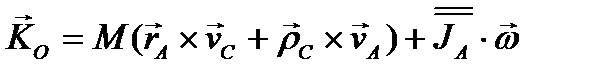. (3.58)

Если за полюс взять центр инерции твердого тела, то

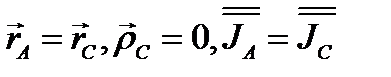
и формула (3.58) упрощается

.

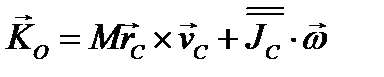Если твердое тело вращается вокруг неподвижной точки О, то

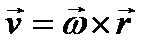
и в результате имеем

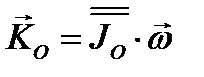(3.59)

Умножая тензор инерции скалярно на вектор угловой скоро­сти 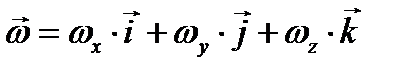(так как тензор инерции симметричен, то его можно умножать на вектор 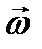как слева так и справа)получаем развернутое представле­ние формулы (3.59)

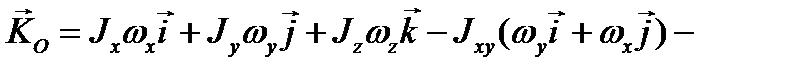
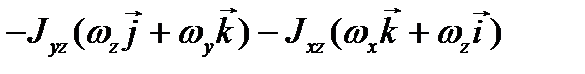(3.60)

Из этого последнего представления сразу следуют выра­жения для кинетических моментов твердого тела относитель­но координатных осей:

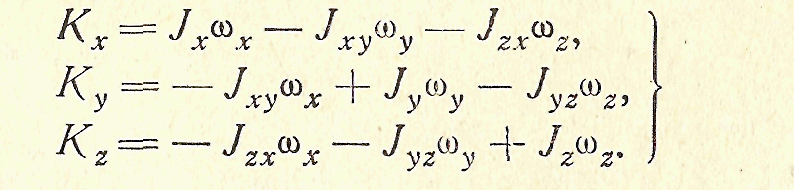(3.61)

Тензорная формула (3.59) является краткой записью этих соотношений. Если оси х, у, z главные, то центробежные мо­менты инерции равны нулю и формулы (3.60) и (3.61) для этого слу­чая упрощаются:

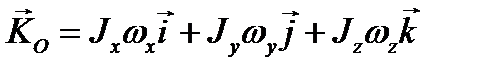Из формул (3.62) отчетливо видно, что кинетический мо­мент тела, вращающегося вокруг точки, не совпадает по на­правлению с вектором его угловой скорости; такое будет иметь место лишь в случае, когда тензор инерции явля­ется шаровым тензором.

Если твердое тело вращается вокруг неподвижной оси, например, оси z, то 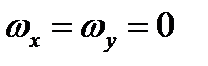и формула (3.60) дает

.

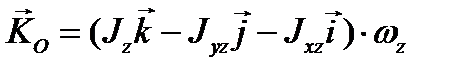Вопросы для самопроверки.

1. Векторная формула кинетического момента системы точек.

2. Теорема об изменении кинетического момента.

3. Дайте определения центральной и главной оси инерции.

4. Чему равен момент инерции цилиндра относительно его продольной оси симметрии?

5. Напишите векторное выражение для кинетического момента тела, вращающегося вокруг неподвижной оси ( варианты- 0X, 0Y, 0Z).

6. Напишите формулу Гюйгенса.

7. Как изменится центробежный момент инерции Jyz при переходе от старой оси OZ к новой, пересекающей ось 0Y на расстоянии l.

8. Напишите формулу тензора инерции относительно выбранного центра (в диадной форме).

9. Как записать момент инерции относительно оси, заданной ортом 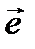, если известен тензор инерции (в общем виде).

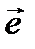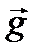10. Как записать центробежный момент инерции относительно осей, заданными ортами и , если известен тензор инерции (в общем виде).

11. Чему равен кинетический момент относительно оси, если 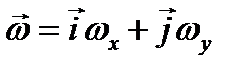, а тензор инерции .

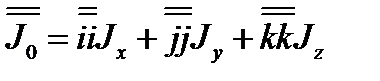12. Чему равен центробежный момент инерции относительно осей, заданными ортами 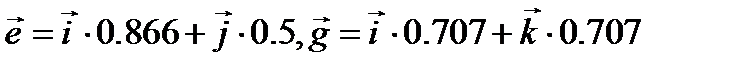, тензор инерции .

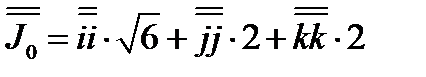Глава 12.