Теорема о движении центра масс.

Рассмотрим другую формулировку теоремы об изменении количества движения. По некоторой аналогии с понятием о центре тяжести твердого тела введем в рассмотрение точку С с вектор-радиусом и назовем эту точку центром масс системы материальных точек.

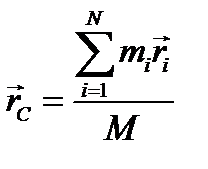(3.18)

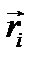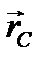Понятие центра масс является более общим, чем понятие центра тяжести: в отличие от понятия центра тяжести понятие центра масс не связано во-первых с наличием каких- либо сил, а во-вторых вектора и не являются постоянными величинами. Взяв производную по времени от обеих частей равенства (3.18), определяющего вектор-радиус центра масс, получим

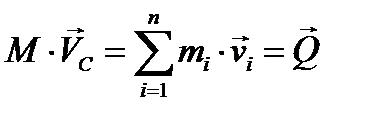(3.19)

где 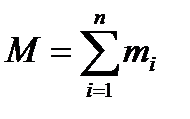- масса всей системы, откуда следует, что количество движения системы материальных точек равно произведению массы системы на скорость движения ее центра масс, или, иными словами, количеству движения цен­тра масс, в котором предположена сосредоточенной вся масса системы. Дифференцируя (3.19) еще раз по времени и вспоминая тео­рему количества движения (3.17), будем иметь

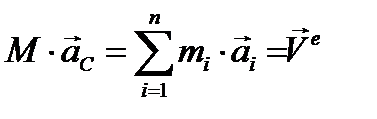(3.20)

Отсюда вытекает теорема о движении центра масс: центр масс системы движется как точка, в которой сосредо­точена вся масса системы и к которой приложен главный вектор внешних сил, действующих на систему. Из приведенной формулировки следует, что внутренние силы не влияют на движение центра масс; только внешние силы мо­гут изменять его движение. Если система находится в покое, то внутренними силами нельзя вывести из покоя ее центр масс; вызванное внутренними силами движение системы будет про­исходить так, что центр масс останется неподвижным. Точно так же, если центр масс находился в движении, то внутренними силами нельзя изменить его движение.

Остановимся на некоторых частных случаях движения си­стемы.

1. Главный вектор внешних сил равен нулю. В этом случае из уравнения (3.19) следует, что центр масс находится в покое или движется прямолинейно и равномерно. Будет ли иметь место покой или движение, за­висит от начальных условий. Пусть система находилась в покое. Дважды интегрируя уравнение (3.19) имеем

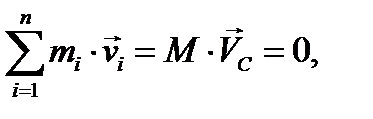
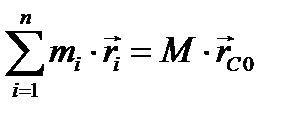
или, введя 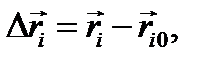получим 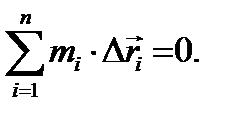Необходимо помнить, что во всех общих теоремах динамики перемещения, скорости и ускорения должны рассматриваться в неподвижной системе отсчёта, т.е. абсолютными.

2. Рассмотрим движение автомобиля по горизонтальному пути; внутренние силы не могут привести его в движение, так как только внешние силы создают изменение движения центра масс. Этими внешними силами являются: сила тяжести, ре­акции дороги и сопротивление воздуха. Единственной движущей силой является горизонтальная составляющая реакции дороги, т. е. сила трения скольжения меж­ду ведущими колесами и дорогой!! Ведомые колеса, наоборот, лишь тормозят движение. Рассмотрим простейшую модель разгона автомобиля. Возьмём переднеприводную машину, на передние колёса которой приходится 0.6 массы автомобиля, тогда имеем. Зададимся вопросом: каким должен быть коэффициент трения f , чтобы разогнать автомобиль до 100 км/час за 5 секунд? Считая силу трения постоянной и движение равноускоренным, получим 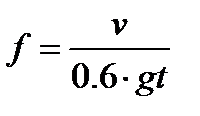, а после подстановки чисел 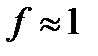. Обычно коэффициент силы трения колеса и шоссе принимают равной в пределах f=0.6-0.8. В рассматриваемой модели не учитывается сопротивление воздуха, торможение ведомых колёс и трение качения. Учёт этих сил увеличивает необходимый для разгона коэффициент трения.

Вопросы для самопроверки/

φ(t)

X

Y

M,l

M,l

M2

1.Напишите формулу центра масс системы.

2.Сосчитайте положение центра масс шатунно-кривошипного механизма, указанного на рисунке в функции от угла φ(t). Длина каждого стержня L.

3. Теорема об изменении главного вектора количества движения .

4. Сформулируйте теорему о движении центра масс.

5. Сформулируйте теорему об изменении главного вектора количества движения.

6. Какому условию должны удовлетворять перемещения системы в случае, если главный вектор внешних сил равен 0.

7. Как переместится центр доски, лежащей на горизонтальном полу, если стоящие по краям люди массами М1, М2 поменяются местами на длину L. Трение между доской и полом отсутствует, масса доски М3.

Глава 11.