Момент инерции относительно произвольной оси. Тензор инерции.

Введенные формулами (3.26), (3.27) величины оказываются существенно необходимыми при изучении динамики вращательных движений твердого тела или системы тел. Эти характеристики инерции зависят как от положения начала координат, так и от направлений выбранных коор­динатных осей. Однако в данной точке тела шесть величин 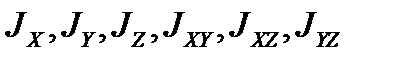вместе с суммарной массой М пол­ностью определяют его инерцию. Иначе говоря, зная эти ве­личины, можно найти момент инерции относительно оси про­извольного направления и центробежный момент инерции для пары новых (повернутых) осей, а также, при известной геометрии тела, перейти к инерционным характеристикам, определенным для другого начала координат. Пусть требуется найти момент инерции относительного заданного направления (оси ξ), характеризуемого ортом 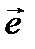. Моментом инерции системы материальных точек относи­тельно оси называется сумма произведений масс этих точек на квадраты их расстояний до оси

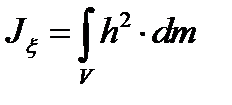
Легко сообразить, что квадрат расстояния h, , можно подсчи­тать по формуле (рис. 53)

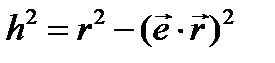(3.28)

где 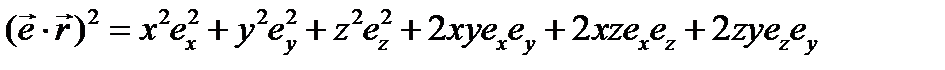3.28а)

Запишем полученное выражение (3.28) иначе

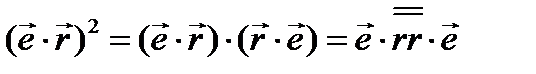(3.29)

О

Х

Y

Z

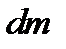
h

ξ

Рис.53

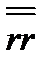Мы изменили порядок сомножителей во втором скалярном произведении и отбросили скобки; первое делать можно, а второе? При этом появилась новая величина , в которой два вектора перемножаются, но не скалярно и не векторно, а каким-то новым способом; такое умножение на­зываетсядиадным (или тензорным),а само произведение - диадой, которая представляет собой тензор второго ранга. Аналитическое определение тензора состоит в следующем: совокупность Зn величин (в трехмерном пространстве), преобразующихся при повороте координатной системы как произведения n координат, называется тензором n-го ранга. По этому определению диада будет тензором 2-го ранга, вектор -тензором 1-го ранга, а скалярная величина — тензором нулевого ранга. Очевидно, что диада 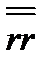не изменится при перестановке ее сомножителей - это симметричная диада. Более общий случай получим, перемножая два разных вектора, например 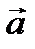и 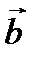; диада 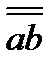уже не будет симметричнойи переставлять сомножители у нее нельзя:

.

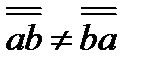Так как векторы 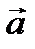и 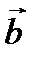можно представить в виде

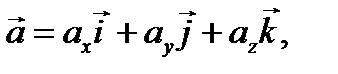
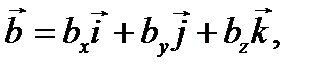
то диада 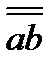может быть записана в виде суммы девяти сла­гаемых

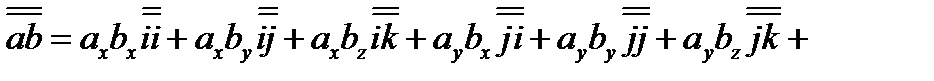
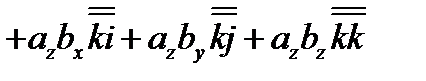(3.30)

Здесь 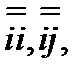….. 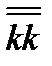элементарные диады, а коэффици­енты при них называются составляющими или компонентами тензора. Тензор второго ранга (диаду) можно записать также в виде квадратной матрицы. Так, для тензора (3.30)

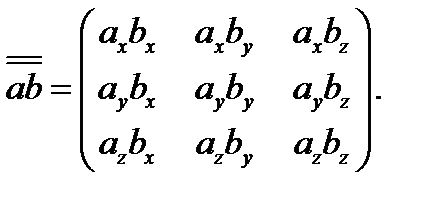(3.31)

Хотя развернутый вид (3.30) тензора 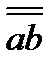и не имеет таблич­ного вида (3.31), однако положение каждой составляющей в таб­лице устанавливается сразу по ее множителю - элементар­ной диаде: левый орт указывает строку, а правый орт - стол­бец, орты соответствуют положению данной составляющей в матрице (3.31). Теперь легко понять неравенство 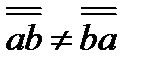; пе­рестановка сомножителей в диаде 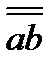означает замену строк столбцами (и наоборот) в матрице (3.31), а тензор 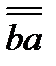будет транспонированным по отношению к первоначальному тен­зору 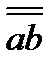. Из теории матриц известно, что квадратную матрицу (3.31) можно умножить справа на вектор-столбец или слева на вектор-строку. Запись тензора в форме (3.30) позволяет эти операции свести к скалярному умножению ортов. Тензор второго ранга 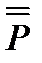можно умножить скалярно как справа, так и слева на вектор а; при этом результат будет различным, так как при правом умножении тензора на вектор будут по­являться скалярные произведения правых ортов элементар­ных диад на орты вектора, а при левом умножении вектора на тензор в скалярных произведениях будут участвовать левые орты элементарных диад. В результате останутся орты элементарных диад, которые не участвовали в скаляр­ных произведениях, поэтому скалярное произведение тензора и вектора будет векторной величиной. Легко сообразить, что 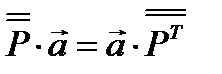, где 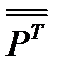означает транспонированный тензор. В случае сим­метричного тензора транспонированный тензор равен перво­начальному и разница между правым и левым произведени­ями исчезает. В нашем случае 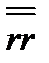симметричный тензор и его разверну­тое выражение типа (3.29) оказывается проще:

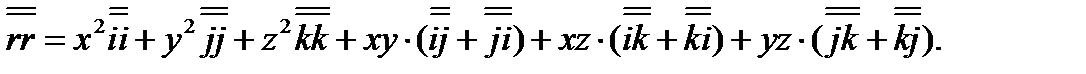(3.32)

Если тензор (второго ранга) умножать скалярно на век­торы и слева, и справа, то участвовать в скалярных произве­дениях будут как левые, так и правые орты элементарных диад, и в результате получится скалярная величина. Именно это мы имеем в формуле (3.29). Записывая эту формулу в виде

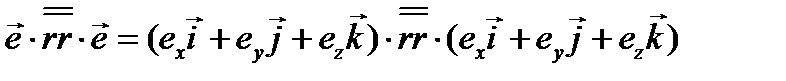, (3.33)

где тензор 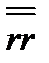представлен выше в виде (3.32), сразу понимаем, что в результате двойного скалярного перемножения в (3.33) исчезают те слагаемые, в которых встречаются произведе­ния (скалярные) разных ортов. Остающиеся слагаемые легко написать сразу; это будут те же компоненты тензора 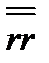,что и представленные в формуле (3.32), только орты в этой фор­муле следует заменить на соответствующие проекции вектора 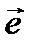. Тогда получим

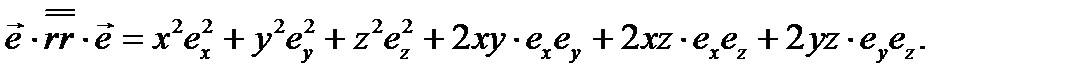(3.34)

Сравнивая результат (3.34) с формулой (3.28а), убеждаемся и законности опускания скобок в формуле (3.29). Простейшим тензором второго ранга будет единичный тензор:

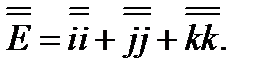(3.35)

Нетрудно сообразить, что диагональные элементы мат­рицы, соответствующей тензору (3.35), будут единицами, а остальные, недиагональные — нулями. Название «единич­ный тензор» совершенно оправдано, так как, умножая на него любой вектор 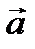(справа или слева - это безразлично), мы опять получим вектор :

=

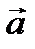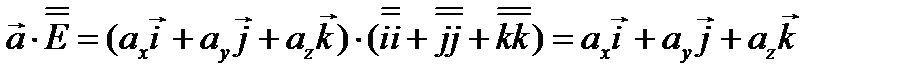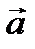
Это свойство единичного тензора 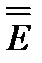приводит к следую­щему интересному соотношению:

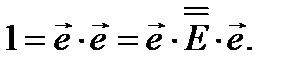(3.36)

Соотношения (3.36) и (3.29) позволяют написать формулу (3.28) В ином виде

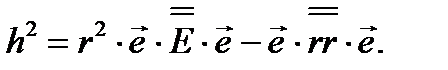(3.37)

Далее, подставляя эту формулу в интеграл для 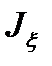, получаем следующее выражение для момента инерции

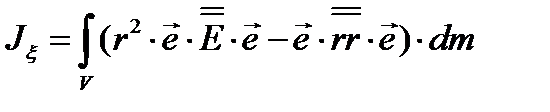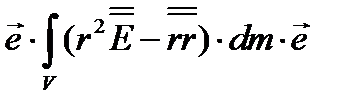= (3.38)

Величина

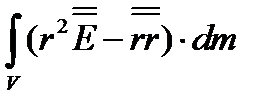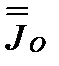= , (3.39)

вошедшая в выражение для 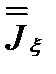(формула 3.38), представляет собой тензор инерции твердого тела в точке О.Вводя этот тензор, переписываем формулу (3.38) для момента инерции относи­тельно оси 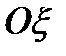, заданной направлением орта 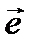, в очень про­стом виде

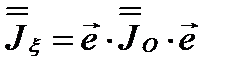(3.40)

Если подставить развернутые диадные представлении тензора 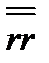и 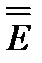в определение тензора 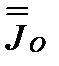и учесть формулы (3.26) и (3.27), получаем диадное представление для тензора инерции

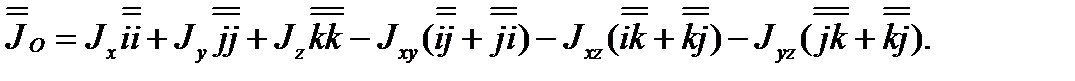(3.41)

Подставим выражение (52) в формулу (51), тогда получим

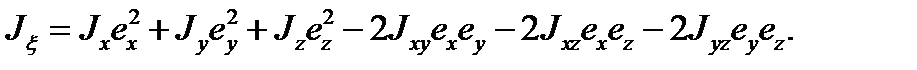(3.42)

Формула (3.40) представляет краткую тензорную запись развернутого представления (3.42). Найдем теперь центробежный момент инерции для пары новых осей 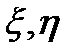, орты которых 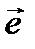и 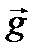перпендикулярны друг другу, т. е. 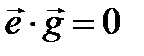. По определению центробежный момент инерции 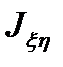равен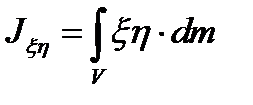

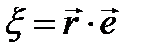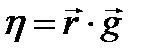Но , а , поэтому

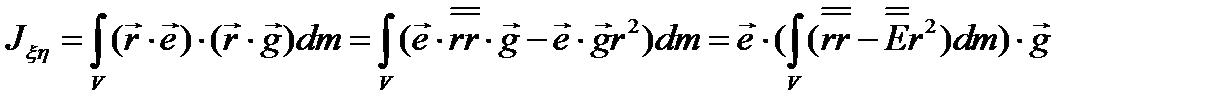Здесь использовано условие ортогональност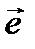и и 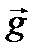и определение единичного тензора 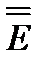. Вспоминая формулу (3.39) для тензора инерции, получаем окончательно

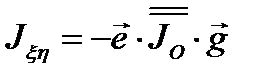. (3.43)

Развёрнутый вид формулы (3.43) получим, произведя фактическое перемножение ортов 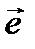, 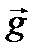и тензора (3.41): 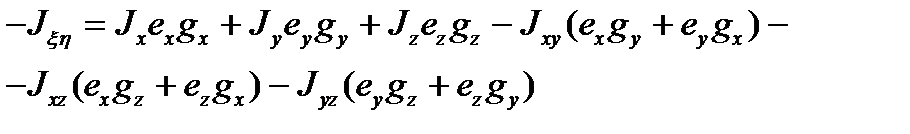(3.44)