Теорема об изменении количества движения системы материальных точек.

Положение системы материальных точек 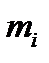(i = 1, 2,..., п) будем определять вектор-радиусами 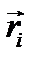этих точек относительно неподвижного начала коорди­нат О; скорости и ускорения точек системы обозначим соответственно через 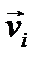, 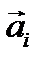. Тела, не включаемые в рассматриваемую систему, назовем внешними по отношению к системе. Такое разделение тел на входящие в систему и не входящие в нее зависит от способа рассмотрения. Мы можем (и в дальнейшем будем так неоднократно поступать) то включать некоторые тела в данную систему, то исключать их из этой системы. Таким образом, силы, приложенные к данной системе, мы разбиваем на две категории:

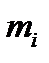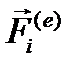1) внутренние силы — силы взаи­модействия материальных точек, входящих в данную систему, и 2) внешние силы — силы взаимодействия системы с телами внешними по отношению к системе. Обозначим равнодействующую всех внешних сил, приложен­ных к точке через , а всех внутренних — через 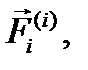тогда дифференциальные уравнения движения системы материальных точек могут быть представлены совокупностью основных урав­нений динамики для отдельных точек системы

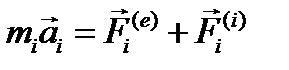(3.14)

Уравнения (3.14) образуют систему Зп обыкновенных дифференци­альных уравнений второго порядка с Зп неизвестными величи­нами 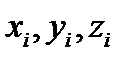, которые должны быть определены как функции времени. Начальные условия, необходимые для определения произвольных постоянных интегрирования, представляют сово­купность начальных условий для каждой точки системы в от­дельности. Современные средства вычислительной техники позволяют получать решения, непосредственно интегрируя уравнения (3.14) для систем, содержащих более миллиона точек. Однако, есть общие теоремы механики, позволяющие упростить решение системы уравнений (3.14) и получить при этом интересные результаты.

Введём вектор 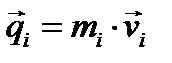, называется количеством движения точки ( в физике импульс). Вектор 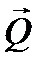, равный

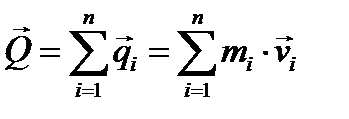(3.15)

называют главным вектором количества движения системы. Складывая вектора количества движения точки, мы должны получить, следуя правилу Пуансо, не только главный вектор количества движения, но и величину

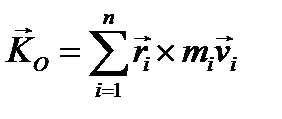, (3.16)

называемую главным моментом количества движения или сокращённо кинетическим моментом.Именно эти две величины вместе определяют движение системы материальных точек и, в частности, движение твёрдого тела в самом общем случае. В зависимости от поставленной задачи, в частных случаях, может быть использована одна из этих величин. Вывод теоремы об изменении количества движения системы, или, как ее кратко называют, теоремы количества движения, основан на идее исключения внутренних сил из дифференциаль­ных уравнений движения системы материальных точек.

Пусть на «i» точку системы действуют внешние и внутренние силы. Продифференцируем (3.15) по времени

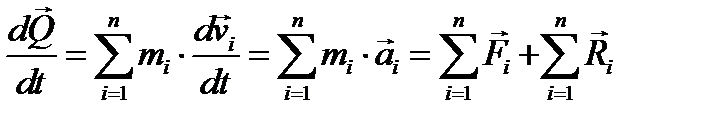
Но последняя сумма, как главный вектор внутренних сил, должна равняться нулю, обозначая 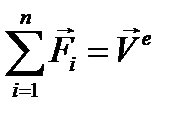, где 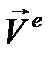- главный вектор внешних сил, получаем

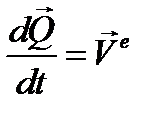(3.17)

Это соотношение выражает теорему об изменении количества движения: векторная производная по времени от главного вектора количества движения системы равна главному вектору внешних сил, приложенных к системе. Равенство нулю главного вектора внутренних сил приводит к заключению, что внутренние силы не могут влиять на измене­ние количества движения системы. Если главный вектор внешних сил равен нулю, т. е. система изолирована от воздействий внешних по отношению к ней тел, то количество движения системы будет сохраняться во времени как по величине, так и по направлению. В этом заключается закон сохранения количества движения.