Теорема об изменении главного момента количества движения системы материальных точек.
Напомним, что момент количества движения системы или кинетический момент определяется выражением
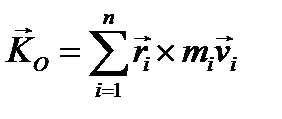 ,
,
Продифференцируем написанное выражение по времени
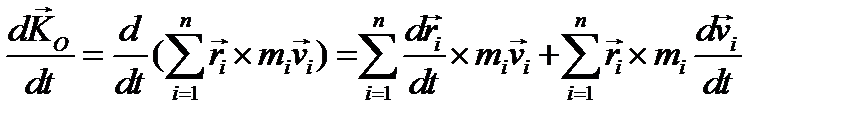
Первое слагаемое равно нулю как векторное произведение равных векторов (ведь 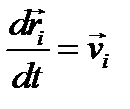 ), а второе, с учётом (3.14) получается равным
), а второе, с учётом (3.14) получается равным
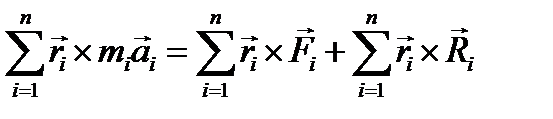
В правой части первое слагаемое – главный момент внешних сил, а второе- главный момент внутренних сил, который равен нулю. Итак, окончательно имеем
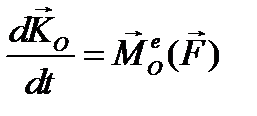 (3.21)
(3.21)
Это соотношение выражает теорему об изменении кинетического момента: векторная производная по времени от главного момента количества движения системы равна главному моменту внешних сил, приложенных к системе. Равенство нулю главного момента внутренних сил приводит к заключению, что внутренние силы не могут влиять на изменение кинетического момента системы.
Формула (3.21) оказываются существенно необходимой при изучении динамики вращательных движений твердого тела или системы тел. С помощью этих двух фундаментальных законов
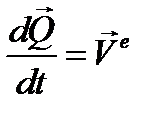
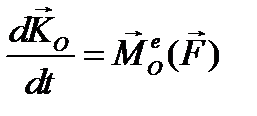 (3.22)
(3.22)
можно получить дифференциальные уравнения движения твёрдого тела и системы тел. В разделе статика указывалось, что необходимыми и достаточными условиями равновесия являлись равенство нулю главного вектора и главного момента сил. Уравнения (3.22) можно переписать в форме, похожей на уравнения статики виде
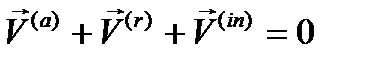
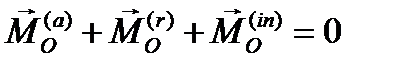
Эти уравнения называютсяуравнениями кинетостатики, где индекс a обозначает активные силы и моменты активных сил, «r»– силы реакций и моменты сил реакций, а индекс « 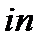 »- силы инерции и моменты сил инерции, которые равны
»- силы инерции и моменты сил инерции, которые равны
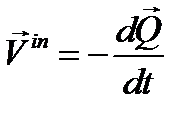 ,
, 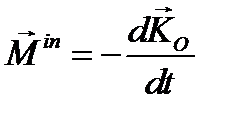 .
.
Дата добавления: 2019-12-09; просмотров: 638;











